这里主要是基于 Denoising Diffusion Probabilistic Models (DDPM) 去做介绍。

基本概念

Diffusion model 的运作方式是：给出一张从高斯分布采样得到的噪声图，经过 T 次的去噪(Denosing)， 最终得到生成的图像。[这个过程也叫做diffusion model 的 reverse process]。

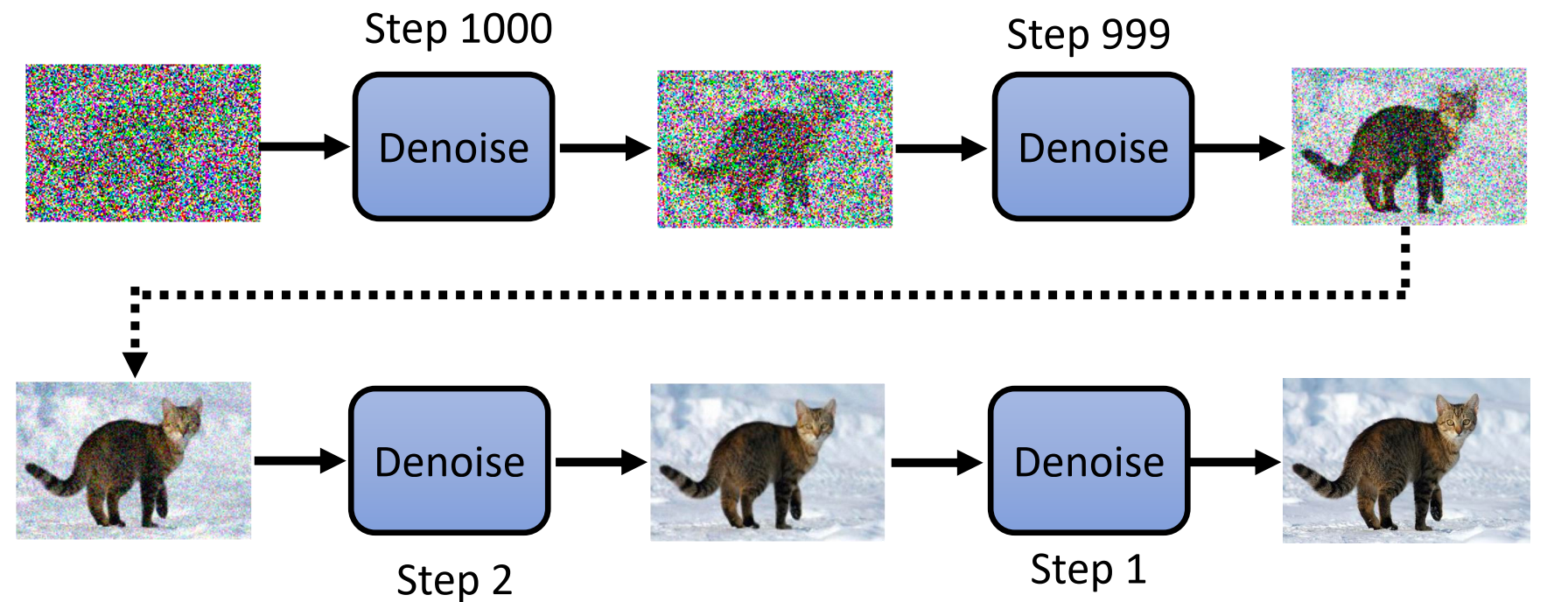
图中所示的 Denoise 模块是同一个网络模块，其输入是一张包含噪声的图像以及当前的 step 数 (step 数的输入非常重要，因为不同的step输入的图像的差距是非常巨大的，denoise 模块需要通过step数来判断输入的图像中的噪声大小)。

当然实际上 Denoise 模块并不是直接让网络就预测输出去除噪声之后的图像， 而是让网络去预测输入图像中的噪声部分，然后输入图像减去预测的噪声得到去噪之后的图像。 (是否可以直接让网络预测输出去噪之后的图像呢？理论上这是可以的， 但是实际上却很少这样子做，因为直接输出去噪之后的图像相对于预测图像中的噪声是更加复杂困难的任务， 这个复杂困难可以从噪声图像的概率分布的复杂性和去噪之后的图像的概率分布的复杂性这个角度去理解)。

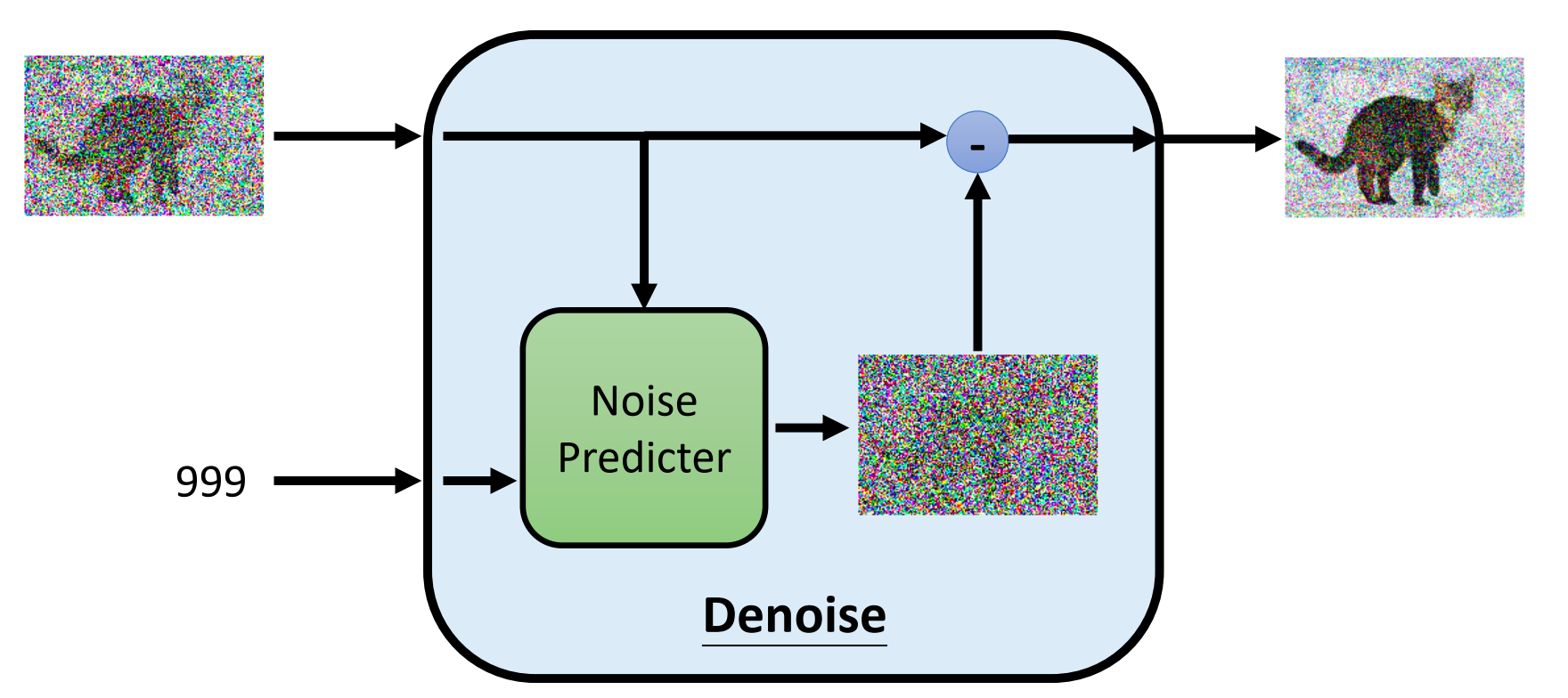
图中的输入只有噪声图像和step number，如果是文生图的应用场景， 则每一步的输入还应该有文本输入（每一步输入的文本都是相同的）。

那么如何训练 noise predictor 呢？ 我们需要的是每个 step 对应的噪声 ground truth，用来监督训练 noise predictor； 我们可以通过往正常的需要生成的图像上一步步加噪声来产生对应的数据对。 这就是diffusion model 的前向过程 (forward process)。

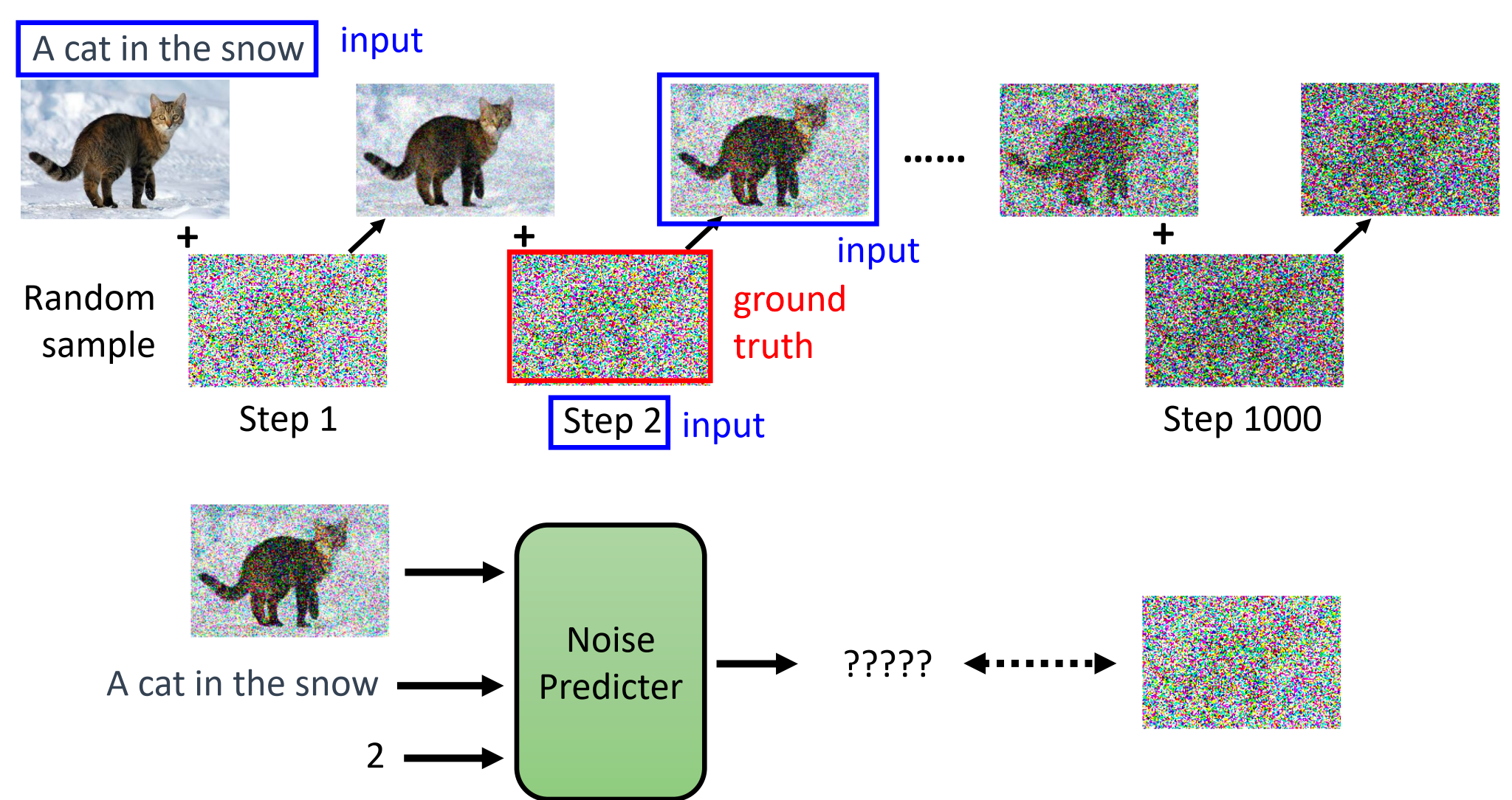
当然，往正常的需要生成的图像上一步步加噪声这个过程，每一步加的噪声的大小是有对应的公式控制，并不是随便加入一个噪声。

DDPM 的完整算法如下图所示； 可以看到，算法伪代码展示的算法过程，跟我们上面介绍的概念是存在一定区别的， 比如加噪声的过程并不是真的一步步加的，而是通过公式直接从$x_0$产生某一步的结果$x_t$; 这是因为在 DDPM 的算法设计和假设中，通过数学化简得到的。

数学原理

前向过程

给定真实图像 $x_0 \sim q(x)$ , diffusion 前向过程通过 T 次对其添加高斯噪声， 得到 $x_1, x_2, \cdots, x_T$。

Diffusion Model 的前向过程的数学定义如下：

具体来说，对于某个时刻 $t$ 与上一个时刻 $t-1$ 的图像均值关系如下：

其中 $\left{ \beta_t \in (0, 1) \right }_{1}^{T}$ 是事先设定好的参数， $\beta_t$ 随着 $t$ 的增大是递增的。前向过程每个时刻 $t$ 都只与 $t-1$ 时刻有关，是一个马尔科夫过程。

实际上，我们可以对加噪声过程进行数学上的变换和化简，从而得到 $x_t$ 与 $x_0$ 的关系， 这对于我们模型的训练效率是十分重要的。令 $\alpha_t = 1 - \beta_t$

因为 $z_1$ 和 $z_2$ 独立同分布(IID)，并且都服从标准高斯分布。 因此(代入高斯分布的概率密度公式化简之后即可得到)：

因此：

其中 $\bar{\alpha} = \alpha_t \alpha_{t-1} \cdots \alpha_0$， 这就是DDPM 算法伪代码中 Training 部分第5行，输入到噪声预测网络$\epsilon_\theta$ 的图像公式。

逆向过程

前向过程(forward process) 是加噪的过程，逆向过程(reverse process)就是去噪的过程， 也是图像生成的过程。如果我们能够逐步得到逆转后的分布$P(x_{t-1} \mid x_t)$ , 就可以从完全的标准高斯分布 $x_T \sim N(0, \mathbf{I})$ 还原得到原图 $x_0$。这个过程的概率密度数学表达式如下：

因为$P(x_{t-1} \mid x_t)$ 是无法通过数学计算出公式解，需要使用神经网络来拟合， 记为 $P_{\theta}(x_{t-1}\mid x_t)$；$\theta$ 代表网络参数。

至此，我们需要回想一下图像生成的本质共同目标：通过某种方式把高斯分布映射到生成结果所构成的概率分布。

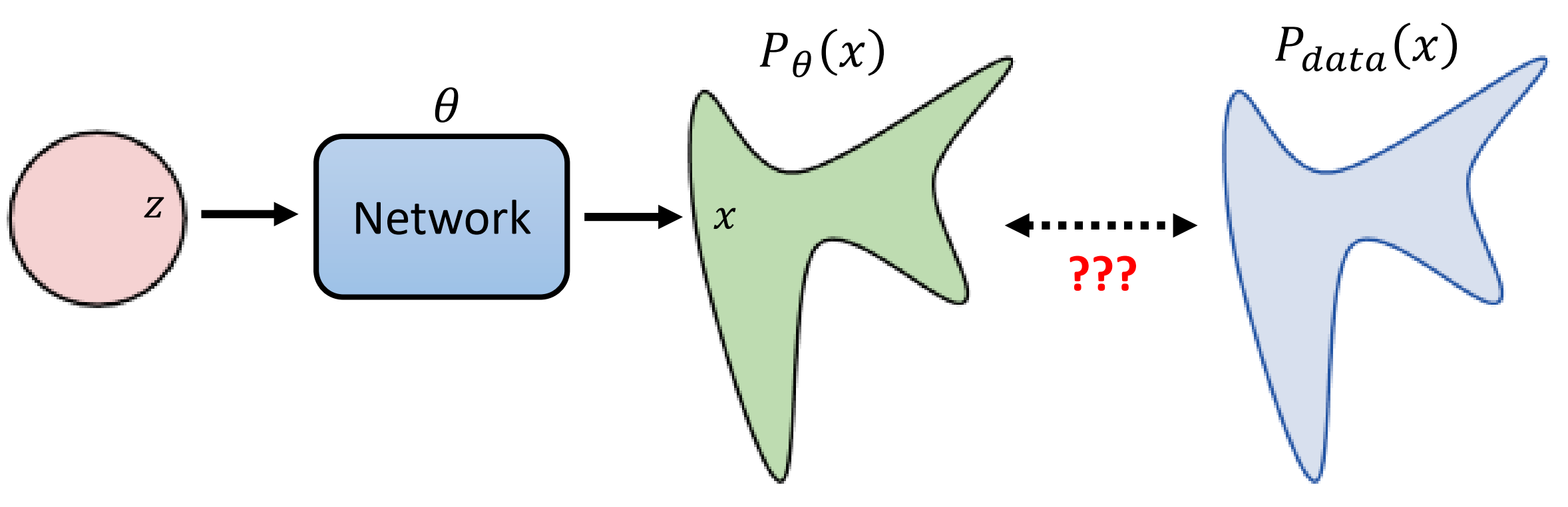
我们需要做的就是，在已经收集的数据上，对 $P_\theta(x)$ 做 maximize likelihood。 对于diffusion model 来说，

对于任意的 $P(x)$ ，都有(跟VAE的部分是一样的)

其中第二项 $\int_z q(z \mid x) \log \left(\frac{q(z \mid x)}{P(z \mid x)}\right) d z$ 即是 KL 散度 $KL\left(q(z\mid x) || P(z \mid x) \right)\geq 0$，因此

$E_{q(z\mid x)}[\log{(\frac{P(x,z)}{q(z\mid x)})}]$ 即是 lower bound。 我们需要maximize 这个 lower bound 从而达到 maximize $\log P(x)$ 的目的。

将VAE 与 DDPM 对应起来，很容易发现，对应于 DDPM，我们需要做的是：

其中 $q(x_{1:T} \mid x_0)$ 就是前向过程(forward process, diffusion process)。

将 $E_{q(x_{1:T} \mid x_0)}\left[\log\left( \frac{P(x_{0:T})}{q(x_{1:T} \mid x_0)}\right)\right]$ 进行变换(化简),

最终我们得到三项相加(减)的结果； 第一项可以认为是重建项，就像在普通 VAE 的 ELBO 中的重建项 $\int_z q(z \mid x) \log P(x \mid z) d z$ 第二项表示diffusion process 的最终分布与标准高斯先验的接近程度，没有可训练的参数，并且在我们的假设下也等于零； 第三项是去噪匹配项，是这里最重要的一项。 diffusion model 的 reverse process 就是希望通过 denoise 模块的 $P_\left(x_{t-1} \mid x_t\right)$ 去拟合去噪步骤的ground truth $q\left(x_{t-1} \mid x_t, x_0\right)$ ，即如下图所示

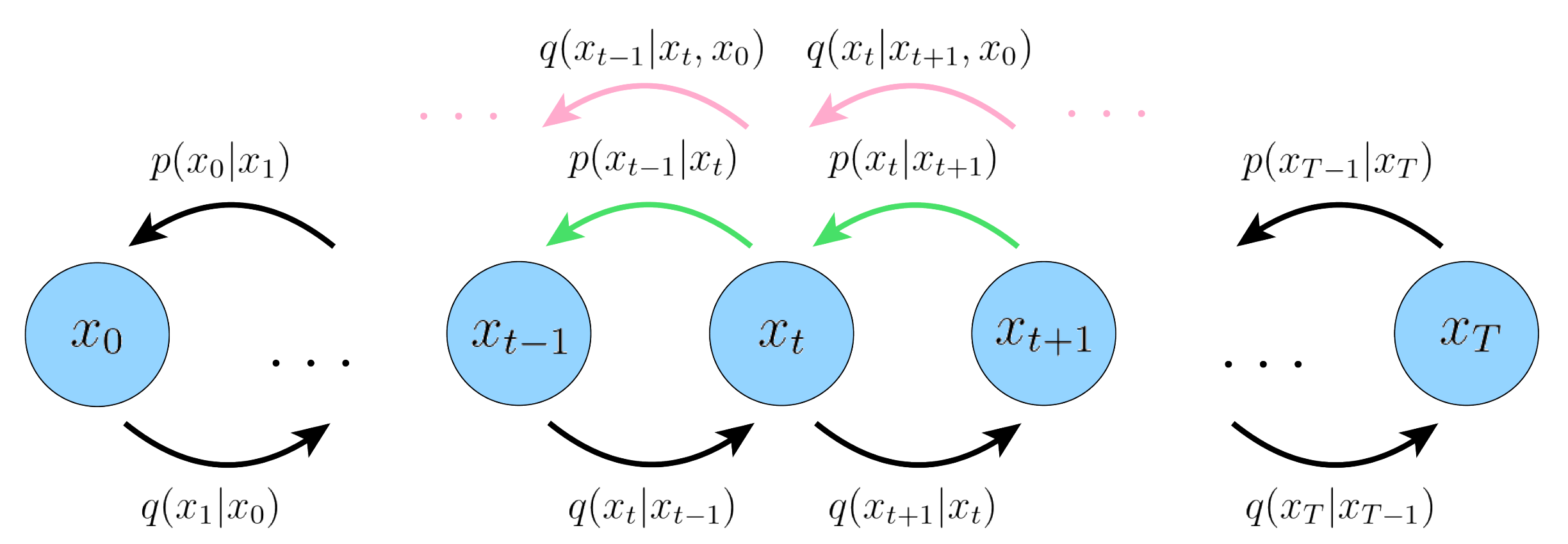
因此我们需要把 $q\left(x_{t-1} \mid x_t, x_0\right) $ 计算出来，利用贝叶斯概率公式

最右边一项能够化简是因为 \(q\left(x_t \mid x_{t-1}, x_0\right) = q\left(x_t \mid x_{t-1}\right)\)， 即forward process 满足马尔科夫性质。 而到这一步，$q\left(x_t \mid x_{t-1}\right)$ ， $q\left(x_{t-1} \mid x_0\right)$ 和 $q\left(x_t \mid x_0\right)$ 都是已知的概率分布， 将概率密度公式代进去硬算可以得到 $q\left(x_{t-1} \mid x_t, x_0 \right)$ 服从分布如下

我们的目标是最小化第三项去噪匹配项，即让两个分布的KL散度最小， 就是希望通过 denoise 模块的 $P_\left(x_{t-1} \mid x_t\right)$ 去拟合去噪步骤的ground truth $q\left(x_{t-1} \mid x_t, x_0\right)$ $q\left(x_{t-1} \mid x_t, x_0\right)$ 是一个高斯分布，而我们对 $P_\left(x_{t-1} \mid x_t\right)$ 的网络输出就是高斯分布的均值，方差一般不考虑。

因此KL散度最小化即是让网络输出的均值跟 $q\left(x_{t-1} \mid x_t, x_0\right)$ 的均值 \(\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right) x_t + \sqrt{\bar{\alpha}_{t-1}}\left(1-\alpha_t\right) x_0}{1-\bar{\alpha}_t}\) 越接近越好。

我们对上述均值式子进一步化简，将 $x_0$ 使用 $x_t$ 替换，我们在前面已经推导出

将 $x_0$ 表示成 $x_t$ 的表达式并使用 $\epsilon$ 来替代 $\bar{z}_t$ 表示噪声

将上式带入 $q$ 的均值式子并化简可以得到

而这里实际需要要网络预测的部分只有 $\epsilon$，因此diffusion model 只需要预测加入的噪声， 并通过上式就可以计算出 $x_{t-1}$ 的图像 这也是diffusion model 算法伪代码的 smapling 的第四行的第一部分的式子。