图像生成-VAE

2023-06-17

基本概念

对于普通的Auto Encoder，其框架如下图所示。

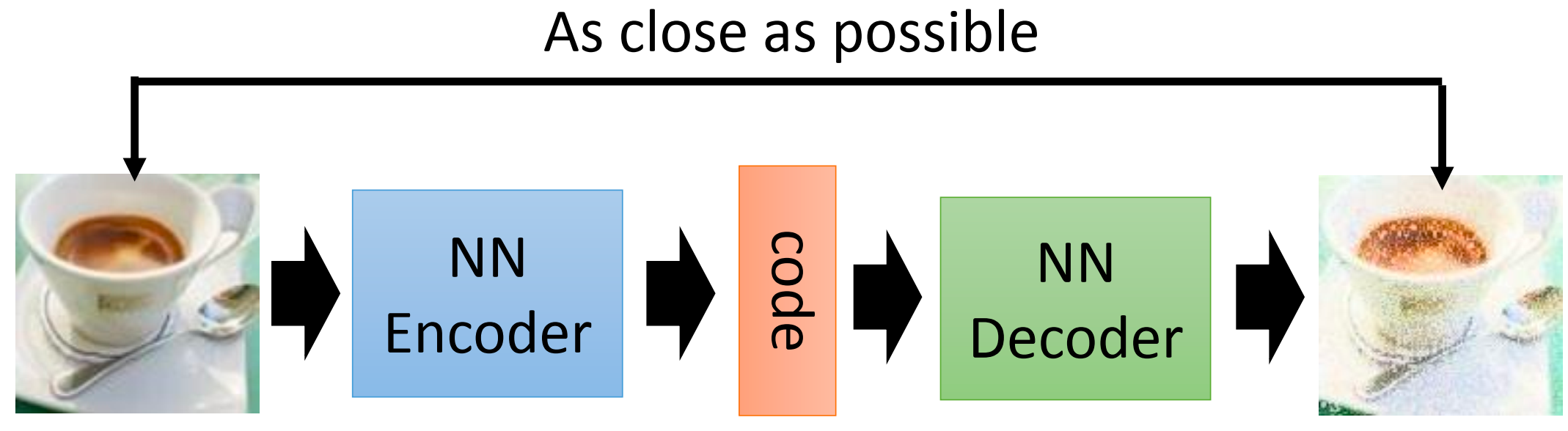
Auto Encoder

输入一张图像，经过 encoder 编程一个特征向量(code)；然后这个 code 经过一个 decoder 之后输出一张图像。在训练的时候， decoder 输出的图像会跟 encoder 输入的图像计算 loss (reconstruction loss)；即是说，我们希望 auto encoder 的 decoder 输出跟 encoder 输入完全一样。一般来说，auto encoder 的作用（目的）就是对信息进行压缩表达。

如果我们可以从某个概率分布随机采样一个 code，或者说从连个已知的 code 之间做插值得到一个新的 code，输入给 decoder，它可以生成一张清晰的图像，那这不就是我们要做的生成式任务吗？但是如果按照原本的 auto decoder 的方式训练的 decoder，显然是不可能做到这件事的；我们随机给一个 code 输入到 decoder，输出大概率是一张模糊的噪声图像。

VAE就是来解决这个问题，它的基本算法框架如下：

VAE

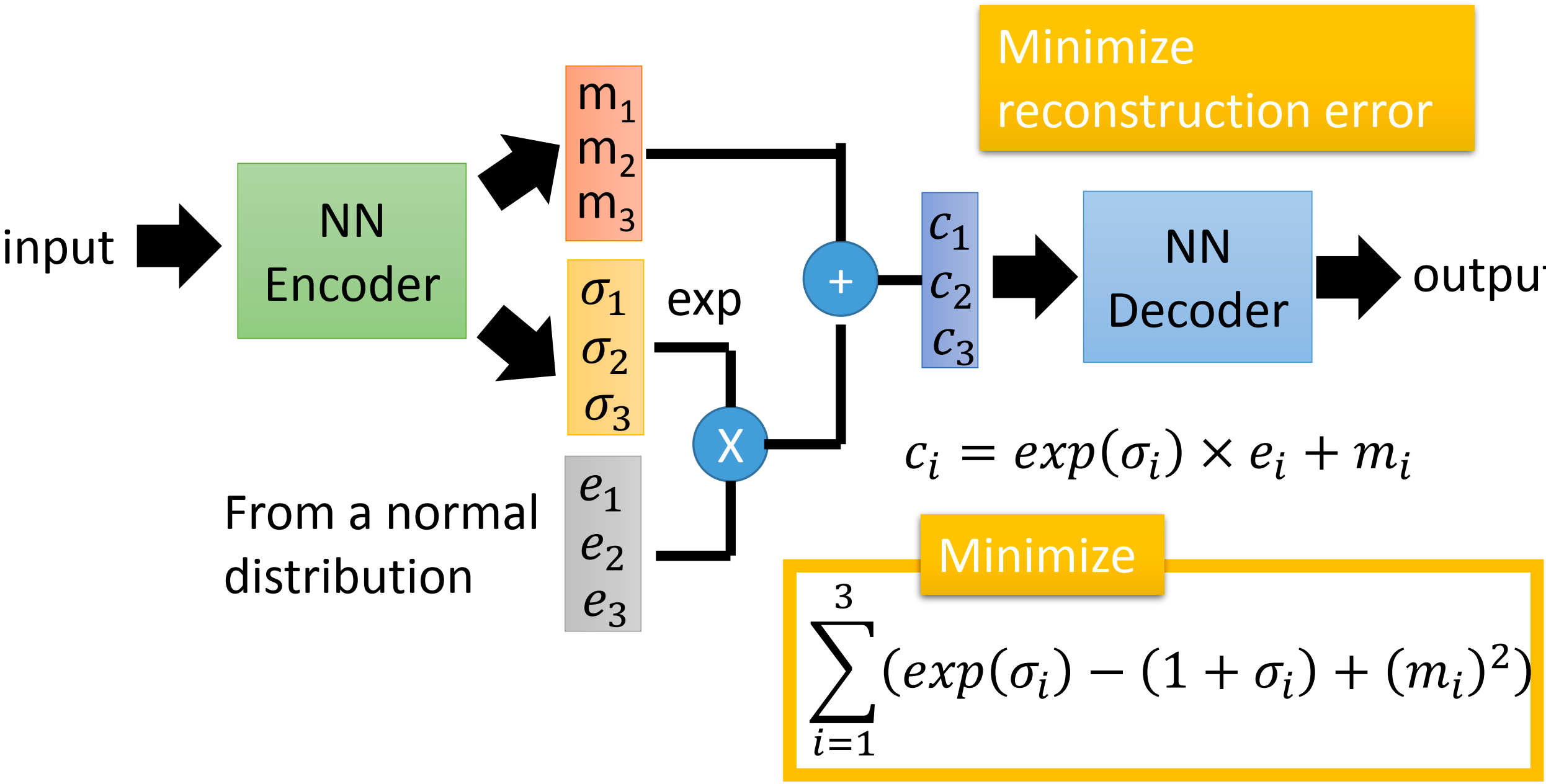
相比原来的 Auto Encoder，VAE 对 code 进行了改变： Encoder 输出一个编码向量$(m_1,m_2,\cdots,m_n)$ 和方差向量$(\sigma_1,\sigma_2,\cdots,\sigma_n)$[需要对它取exponential才是真正的方差]。最后输入到 Decoder 的编码是

\[(c_1,c_2,\cdots,c_n) = (m_1,m_2,\cdots,m_n) + exp(\sigma_1,\sigma_2,\cdots,\sigma_n) \times (e_1,e_2,\cdots,e_n)\]

其中$(e_1,e_2,\cdots,e_n)$是从标准正态分布采样的一个向量。

需要注意的是，VAE的training loss 除了 reconstruction error以外，还包括一项对于方差向量$(\sigma_1,\sigma_2,\cdots,\sigma_n)$的约束和一项对于Encoder 输出的编码向量$(m_1,m_2,\cdots,m_n)$的正则化约束；即：

\[\sum_{i=1}^{n} \left(exp(\sigma_i) - (1 + \sigma_i) + (m_i)^2 \right)\]

这一项是至关重要的，因为如果没有这一项，那 Encoder 输出的方差向量（exp之后）直接是0，那么 reconstruction error 肯定是最小的，因为这时各个输入图像之间的编码是最不容易有overlap的。

Why VAE (直观解释）

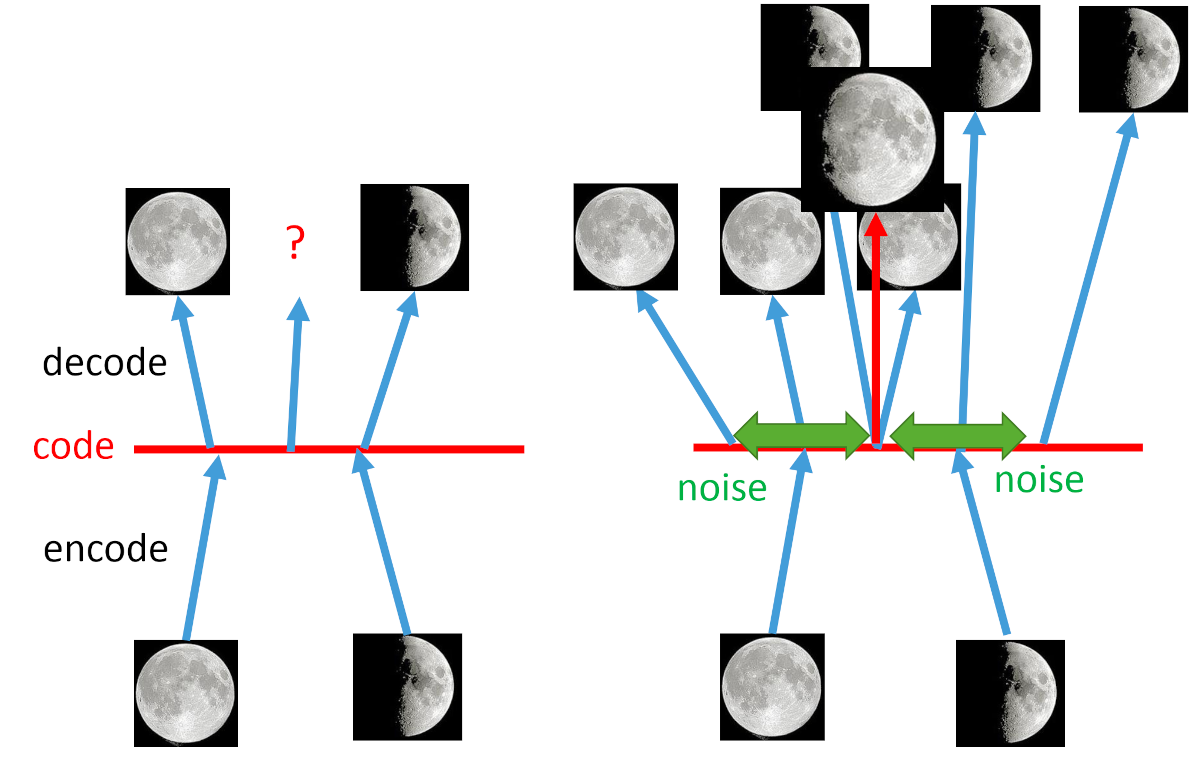
为什么VAE能够实现从编码空间(code space)采样一个编码输入到 Decoder 生成正常的图像呢？

从直观上来说，我们把编码空间用一条直线来表示，那么一个编码(code)就是直线上的一个点。对于原本的 Auto Encoder 来说，其 Encoder 是把图像编码到直线上的一个点，其 Decoder 就是输入直线上的一个点解码为图像；而直线上的两个训练图像的编码点之间的采样点，Decoder 完全没有见过，也没有对编码空间有任何约束(比如平滑/线性等，实际上这些约束也是非常难做的)，因此从编码空间(code space)采样一个编码输入到 Decoder 很大概率是没有办法生成正常清晰的图像的。

VAE 针对编码空间编码点之间的空间，通过加入噪声的方式，使得每个训练的编码点覆盖的范围更加广，甚至不同编码点的覆盖区域会产生 overlap，从而使得 Decoder 训练学习到更多的编码空间；同时，由于编码点的覆盖区域会产生 overlap，从而编码空间对于 Decoder 可能是比较线性/平滑的；这就使得 VAE 能够将从编码空间(code space)采样的编码恢复出正常的图像。

intuitiveVAE

Why VAE (数学解释）

回到图像生成的目标： 找到一个合适的概率分布，从概率分布中采样得到新的图像。 而这个概率分布往往通过某种方式把高斯分布映射到生成结果所构成的概率分布。

我们可以认为所需要的概率分布是一个连续空间的 infinite 混合高斯模型，即：

\[z \sim N(0, I) , \quad x \mid z \sim N(\mu(z), \sigma(z)) \\ P(x) = \int_z P(z)P(x \mid z) dz\]

其中 $z$ 是一个向量，每个元素都服从高斯分布；值得一提的是，虽然 $z$ 是服从一个简单的高斯分布，但是 $P(x)$ 可以是非常复杂的概率分布；同时，$z$ 也可以不是高斯分布，可以是其他的概率分布，其概率分布不影响最终的结果。

$\mu(z), \sigma(z)$ 表示给定 $z$ 的情况下，$x \mid z$ 所服从的高斯分布的均值和方差， $\mu(z), \sigma(z)$ 均是需要估计(学习)的；

那么，对于收集到的数据 $X = {x}$，我们的目标是 maximize $P(x)$ ，即极大似然：

\[\max L = \max \sum_{x} \log P(x)\]

引入一个任意概率分布 $q(z \mid x)$ ，下式永远成立:

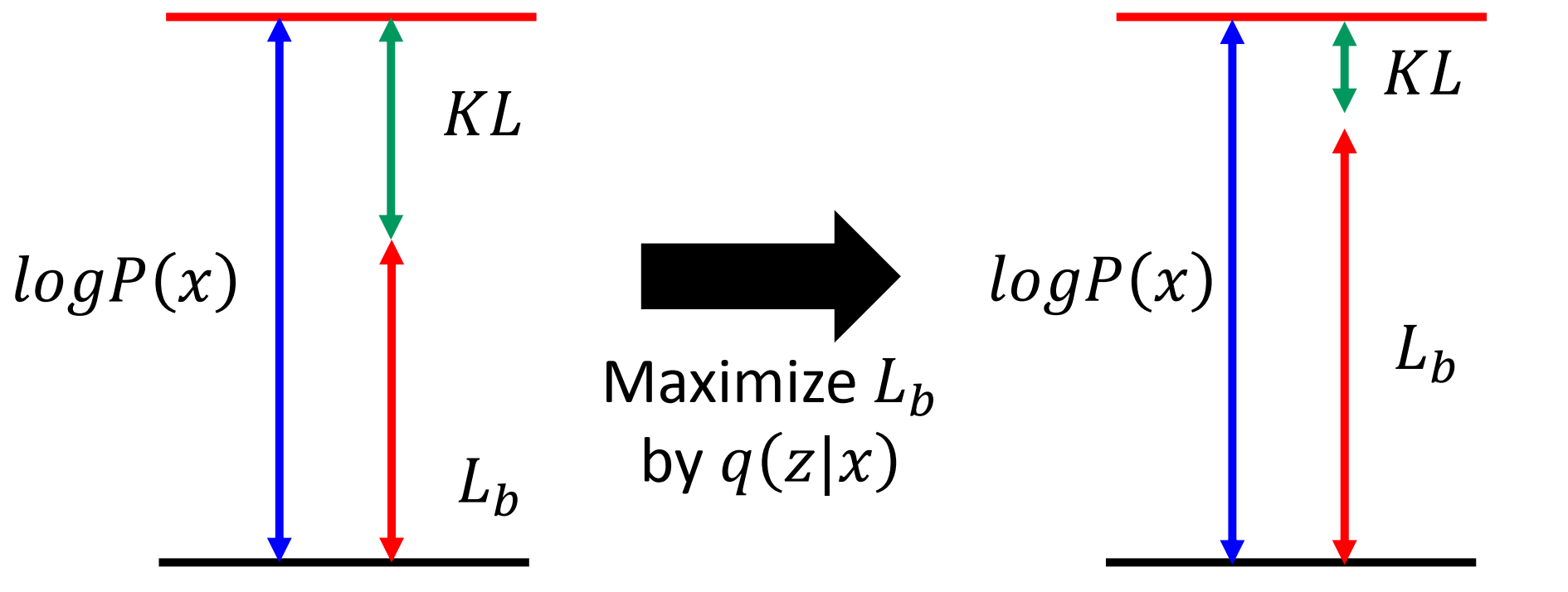
\[\begin{aligned} & \log P(x)=\int_z q(z \mid x) \log P(x) d z \quad 【q(z \mid x) \text { can be any distribution }】 \\ & =\int_z q(z \mid x) \log \left(\frac{P(z, x)}{P(z \mid x)}\right) d z= \int_z q(z \mid x) \log \left(\frac{P(z, x)}{q(z \mid x)} \frac{q(z \mid x)}{P(z \mid x)}\right) d z \\ & =\int_z q(z \mid x) \log \left(\frac{P(z, x)}{q(z \mid x)}\right) dz + \int_z q(z \mid x) \log \left(\frac{q(z \mid x)}{P(z \mid x)}\right) d z \\ \end{aligned}\]

其中第二项 $\int_z q(z \mid x) \log \left(\frac{q(z \mid x)}{P(z \mid x)}\right) d z$ 即是 KL 散度 $KL\left(q(z\mid x) || P(z \mid x) \right)\geq 0$，因此

\[\log P(x) \geq \int_z q(z \mid x) \log \left(\frac{P(x \mid z) P(z)}{q(z \mid x)}\right) d z = E_{q(z\mid x)}[\log{(\frac{P(x,z)}{q(z \mid x)})}]\]

$\int_z q(z \mid x) \log \left(\frac{P(x \mid z) P(z)}{q(z \mid x)}\right) d z$ 即是 $\log P(x)$ 的 lower bound $L_b$。

重新将极大似然的式子书写如下：

\[\log P(x) = L_b + KL\left(q(z\mid x) || P(z \mid x) \right)\]

希望通过最大化 $L_b$ 来使得 $P(x)$ 最大；即同时寻找 $P(x\mid z)$ 和 $q(z \mid x)$ 使得最大化 $L_b$ 来使得 $P(x)$ 最大。

值得注意的是，因为 $P(x)$ 跟 $P(z \mid x)$ 是没有关系的，因此在这个过程中，由于 $q(z \mid x)$ 的引入，会使得优化后的 $KL\left(q(z\mid x) || P(z \mid x) \right)$ 也是最小的，即 $q(z \mid x)$ 是 $P(z \mid x)$ 的一个近似分布。

log likely

\[\begin{aligned} & L_b=\int_z q(z \mid x) \log \left(\frac{P(z, x)}{q(z \mid x)}\right) d z= \int_z q(z \mid x) \log \left(\frac{P(x \mid z) P(z)}{q(z \mid x)}\right) d z \\ & =\int_z q(z \mid x) \log \left(\frac{P(z)}{\sqrt{q(z \mid x)}}\right) d z+ \int_z q(z \mid x) \log P(x \mid z) d z \end{aligned}\]

其中，第一项 $\int_z q(z \mid x) \log \left(\frac{P(z)}{\sqrt{q(z \mid x)}}\right) d z$ 是负的 KL 散度：$-KL(q(z\mid x) || P(z))$；第二项可以认为是重建项。因此，需要 minimize $KL(q(z\mid x) || P(z))$， maximize $\int_z q(z \mid x) \log P(x \mid z) d z$。