NeRF 入门原理介绍

2023-04-08

前奏: 神经网络隐式表面表示

Occupancy networks

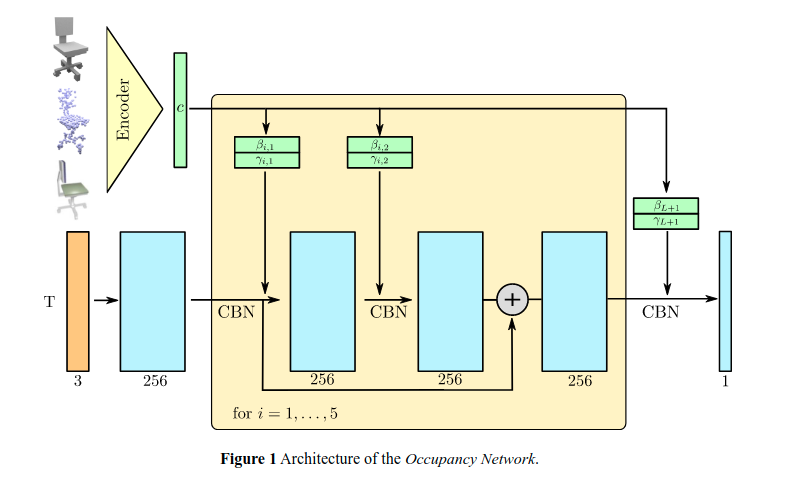
希望通过网络拟合一个函数 $f_\theta^x : R^3 \rightarrow [0, 1]$。$x$ 作为函数的一个条件，这里直接把 $x$ (的编码)也当做一个输入。

(注：虽然把 $x$ 也当做一个输入，但是对 $x$ 的使用是一个显式规定的方式，即在CBN里使用。因此确实可以认为 $x$ 就是一个条件)

输入: 特定任务编码器输出的编码 $c\in X=R^C$ 以及一个 batch 的点 T。

输出: $f(c, p_1), \cdots, f(c, p_T) \in [0, 1]$ 。就是说，对于 T 中的每一点，网络会输出一个数。

算法(网络)流程

用一个全连接网络将点 $p_i$ 做编码(Embedding)，得到一个 256 维的特征向量
5 个相同的Block: 以上一个的输出作为输入，通过ONet ResNet-block，输出一个 256 维的特征向量
最后一个 ONet ResNet-block 输出的特征向量进过一个 CBN 层和 ReLU 激活函数
通过一个全连接网络数据一个 1 维的实数
通过 Sigmoid 将输出映射到[0, 1]

Conditional Batch Normalization (CBN) Layer

输入:

$c$, 特定任务编码器输出的编码
上一层网络输出的特征向量: $f_{in}^{i} \quad f_{in}^i \in R^{256}; i\in[1:T]$.

输出: 一个经过normalization 后的特征向量 $f_{out}^i \quad f_{out}^i \in R^{256}; i\in[1:T]$.

流程:

计算输入特征向量的均值和方差, $f_{in}^i \quad {i\in[1:T]}$ over all $i \in [1:T]$. $\mu = E[f_{in}^i], \quad \sigma^2 = Var[f_{in}^i]$
然后使用两个全连接网络从特定任务编码器输出的编码 $c$ 中得到两个 256 维的向量 $\beta(c)$ 和 $\gamma(c)$.
将输入特征向量标准化后再做一次仿射变换 $f_{out}^i = \gamma(c) \frac{f_{in}^i - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta(c)$

ONet ResNet-block

CBN layer;
ReLU activation function;
Fully-connected layer;
CBN layer;
ReLU activation function;
Fully-connected layer;

数据预处理

占用场函数: 给定一个实体形状 $S \subset R^3$，占用场函数 $o: R^3 \rightarrow {0, 1}$.

\[o(p) = \left\{\begin{matrix} 0, \quad p\notin S \\ 1, \quad p\in S\end{matrix}\right.\]

通过占用场函数，将mesh数据转化为占用场数据，用于网络的训练。

Loss

\[\mathcal{L}_{\mathcal{B}}(\theta)=\frac{1}{|\mathcal{B}|} \sum_{i=1}^{|\mathcal{B}|} \sum_{j=1}^{K} \mathcal{L}\left(f_{\theta}\left(p_{i j}, c_{i}\right), o_{i j}\right)\]

其中，$\mathcal{B}$ 是上述预处理数据 $S$ 的一个子集， $\left|\mathcal{B}\right| = 64$

$K$ 是一个shape采样的点数。 $\mathcal{L}$ 是交叉熵损失函数。

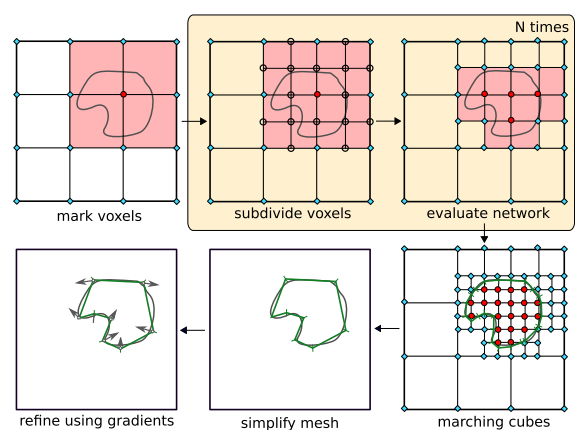
\[\mathcal{L}\left(f_{\theta}\left(p_{i j}, c_{i}\right), o_{i j}\right) = -\left[o_{i j} \log \left(f_{\theta}\left(p_{i j}, c_{i}\right)\right) + \left(1-o_{i j}\right) \log \left(1-f_{\theta}\left(p_{i j}, c_{i}\right)\right)\right]\]

Multiresolution IsoSurface Extraction (MISE)

首先测试给定分辨率下的所有点，这些点已经被评估为占用（红色圆圈）或未占用（青色菱形）。
然后，确定所有具有已占用和未占用的角的体素，并将其标记为active（浅红色），并将它们细分为8个子体素。
接下来，我们评估细分所引入的所有新网格点（空圆）。
重复前两个步骤，直到达到所需的输出分辨率。
最后，使用 marching cube 算法提取网格，使用一阶和二阶梯度信息简化和细化输出网格。

IM-NET

Learning Implicit Fields for Generative Shape Modeling

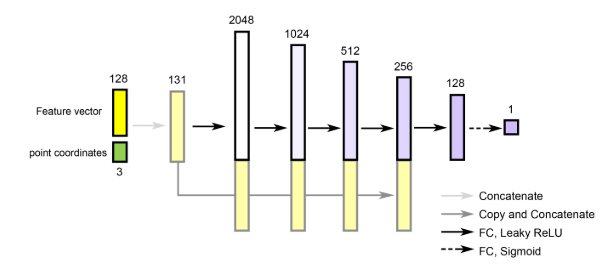
希望通过网络拟合一个函数 $f^x_\theta : R^3 \rightarrow [0, 1]$. $x$ 作为函数的一个条件，这里直接把 $x$ (的编码)也当做一个输入。

(注：这里与Occupancy Net 不同，$x$ 确实仅仅是最为输入，对于 $x$ 信息的使用方式由网络自己决定)

内外场定义: (其实跟Occupancy Net 的占用场是一个东西) $\mathcal{F}(p)=\left\{\begin{array}{ll} 0 & \text { if point } p \text { is outside the shape, } \\ 1 & \text { otherwise. } \end{array}\right.$ 其实就是希望 $f^x_\theta: R^3 \rightarrow \mathcal{F(p)}$ .

数据准备

为了训练这样一个网络，需要的数据是 point-value pair。

使用分层表面预测(HSP)技术将voxel model采样到不同的分辨率。然后从不同的分辨率采用point-value pair。

为了降低采样的复杂度(朴素的采样方法以每个vexel作为中心采样，会产生 $n^3$ 个点)。一种更有效的方法是在形状表面附近对更多的点进行采样，而忽略距离较远的大多数点，从而得出大约 $O(n^2)$ 个点。为了补偿密度变化，我们为每个采样点p分配了权重 $w_p$，它表示 p 附近的采样密度的倒数。

Loss

\[\mathcal{L}(\theta) = \frac{\sum_{p\in S}\left|f_\theta(p) - \mathcal{F}(p)\right|^2 \cdot w_p}{\sum_{p\in S}w_p}\]

DeepSDF

直接回归符号距离函数(SDF), 而不是binary的占用场。 $SDF(\boldsymbol{x})=s; \quad \boldsymbol{x} \in \mathbb{R}^{3}, s \in \mathbb{R}$ $x$ 表示点，$s$ 表示 SDF 的值。

用一个网络来近似 $f_\theta: R^3 \rightarrow R$ 的映射。即 $f_\theta(x) \approx SDF(x)$ 。

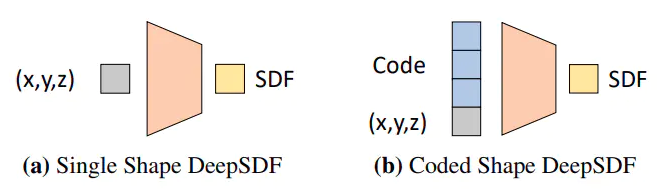
single shape deepSDF

只能对单种 shape 进行重建；因为输入中没有任何关于 shape 的信息，这些信息只能是固化到网络里面。

code shape deepSDF

将 shape 用 latent vector 的方式作为网络的输入，以此来实现不同 shape 的重建

单点的Loss

\[\mathcal{L}\left(f_{\theta}(\boldsymbol{x}), s\right) = \left|\operatorname{clamp}\left(f_{\theta}(\boldsymbol{x}), \delta\right) - \operatorname{clamp}(s, \delta)\right|\]

其实就是预测得到的SDF值与真实SDF之间的一个距离
$\delta$ 参数用于将注意力集中在表面附近

基于概率视角的Loss

对于 $N$ 个 SDF 的形状 $SDF^i_{[1:N]}$ , 从每个shape采样 $K$ 个 point-value pair $X_i = \left\{(x_j, s_j): s_j=SDF^i(x_j)\right\}$ 对于自动解码器，由于没有编码器，因此每个 latent vector $\boldsymbol{z}_i$ 与训练 shape $X_i$ 配对。

给定形状SDF样本 $X_i$, $\boldsymbol{z}_i$ 的后验概率可以表示为： $p_{\theta}\left(\boldsymbol{z}_{i} \mid X_{i}\right) = p\left(\boldsymbol{z}_{i}\right) \prod_{\left(\boldsymbol{x}_{j}, \boldsymbol{s}_{j}\right) \in X_{i}} p_{\theta} \left(\boldsymbol{s}_{j} \mid z_{i} ; \boldsymbol{x}_{j}\right)$

其中 $p\left(\boldsymbol{z}_{i}\right)$ 假设服从zero-mean multivariate-Gaussian分布
使用深度神经网络来近似 SDF likelihood： $p_{\theta}\left(\boldsymbol{s}_{j} \mid z_{i} ; \boldsymbol{x}_{j}\right) = \exp \left(-\mathcal{L} \left(f_{\theta}\left(\boldsymbol{z}_{i}, \boldsymbol{x}_{j}\right), s_{j}\right)\right)$

这样最终得到训练阶段的优化目标： $\underset{\theta,\left\{\boldsymbol{z}_{i}\right\}_{i=1}^{N}}{\arg \min } \sum_{i=1}^{N}\left(\sum_{j=1}^{K} \mathcal{L} \left(f_{\theta}\left(\boldsymbol{z}_{i}, \boldsymbol{x}_{j}\right), s_{j}\right)+ \frac{1}{\sigma^{2}}\left\|\boldsymbol{z}_{i}\right\|_{2}^{2}\right)$ 测试阶段，固定参数 $\theta$ 。估计最大后验概率： $\hat{\boldsymbol{z}}=\underset{\boldsymbol{z}}{\arg \min } \sum_{\left(\boldsymbol{x}_{j}, \boldsymbol{s}_{j}\right) \in X} \mathcal{L}\left(f_{\theta}\left(\boldsymbol{z}, \boldsymbol{x}_{j}\right), s_{j}\right)+ \frac{1}{\sigma^{2}}\|\boldsymbol{z}\|_{2}^{2}$

PIFu

Pixel-Aligned Implicit Function for High-Resolution Clothed Human Digitization Shunsuke

编码器为每个像素学习一个编码，即学习的是 HxWxd 的特征编码，而不是把整个图像编码到一个 1-d 的特征。

然后每个像素的特征作为一个隐式函数 $f(F(x), z(X)): \R^d \rightarrow \R$ 的一个输入。$f$ 是要去预测 X 这个点是在物体里面还是外面。

为每个像素学习一个特征的好处是，原图像域与特征域在空间上是一一对齐的；那么在多视角的时候，可以通过相机光线投射的关系确定哪些像素的特征应该融合。

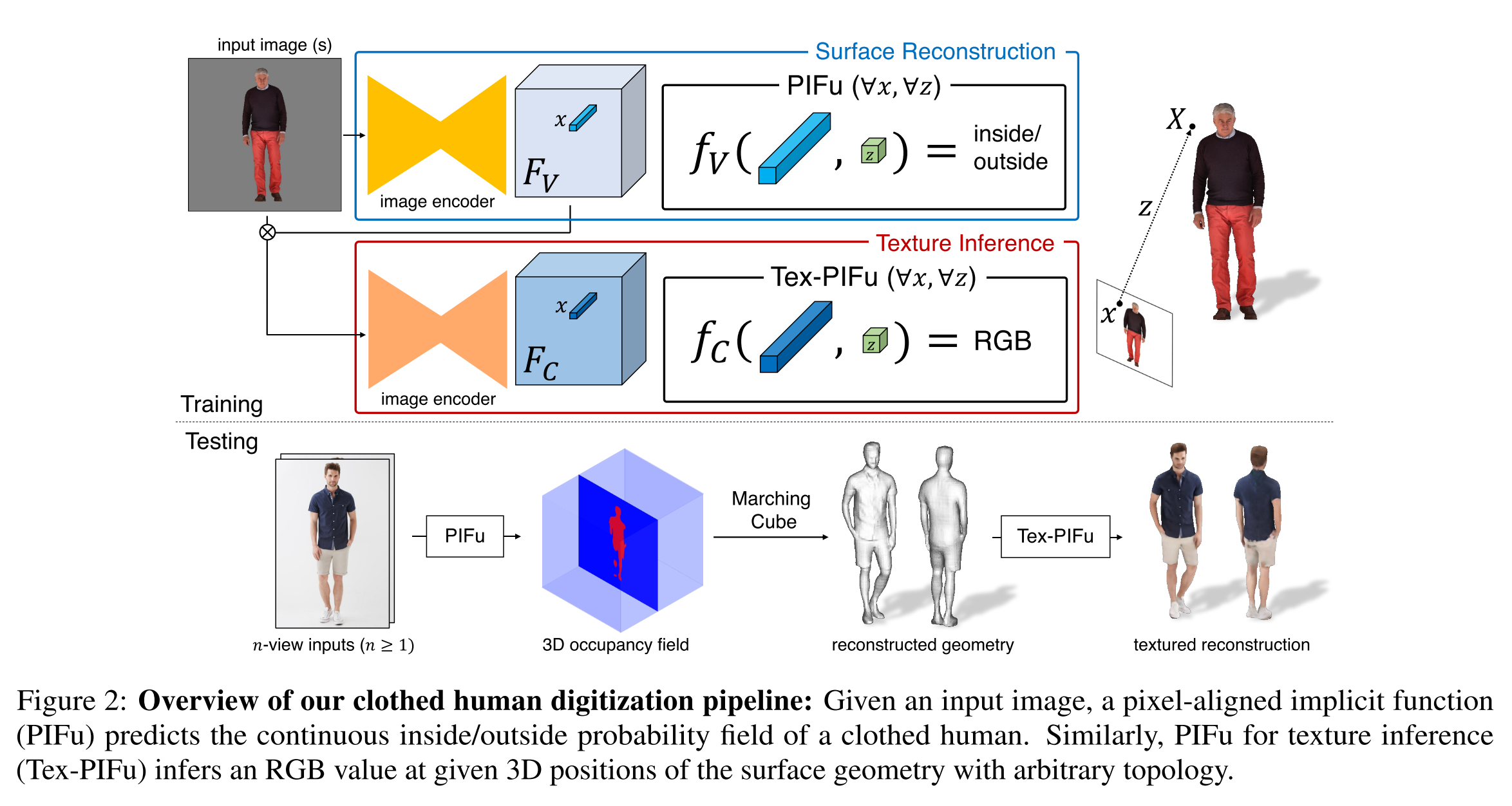
PIFu: Pixel-Aligned Implicit Function

\[f(F(x), z(X))=s: s \in \mathbb{R}\]

$x = \pi(X)$ 是 2D 投影，$z(X)$ 是相机坐标系下的深度值； $F(x)$ 是在 $x$ 位置像素的特征编码；$s$ 是类似于 SDF 的值。

单视角的重建

对于表面重建，将表面表示成一个占用场： $f_{v}^{*}(X)=\left\{\begin{array}{ll} 1, & \text { if } X \text { is inside mesh surface } \\ 0, & \text { otherwise } \end{array} .\right.$ 重建 Loss 为： $\mathcal{L}_{V} = \frac{1}{n} \sum_{i=1}^{n} \left|f_{v}\left(F_{V}\left(x_{i}\right), z\left(X_{i}\right)\right)- f_{v}^{*}\left(X_{i}\right)\right|^{2}$ 这里的 3D 点是通过 ray casting 的方式采样的。

纹理的学习

多视角的重建

主要是将多视角的信息进行融合。因为编码器输出的是每个像素的特征；每个三维点对应到多视角中的那些像素是可以通过相机光线投射的关系得到的，那么对应的特征也就有。把一个三维点的对应的所有视角的有效像素特征拿出，在做融合就可以了。文中用的是average pooling 的方式来融合的。

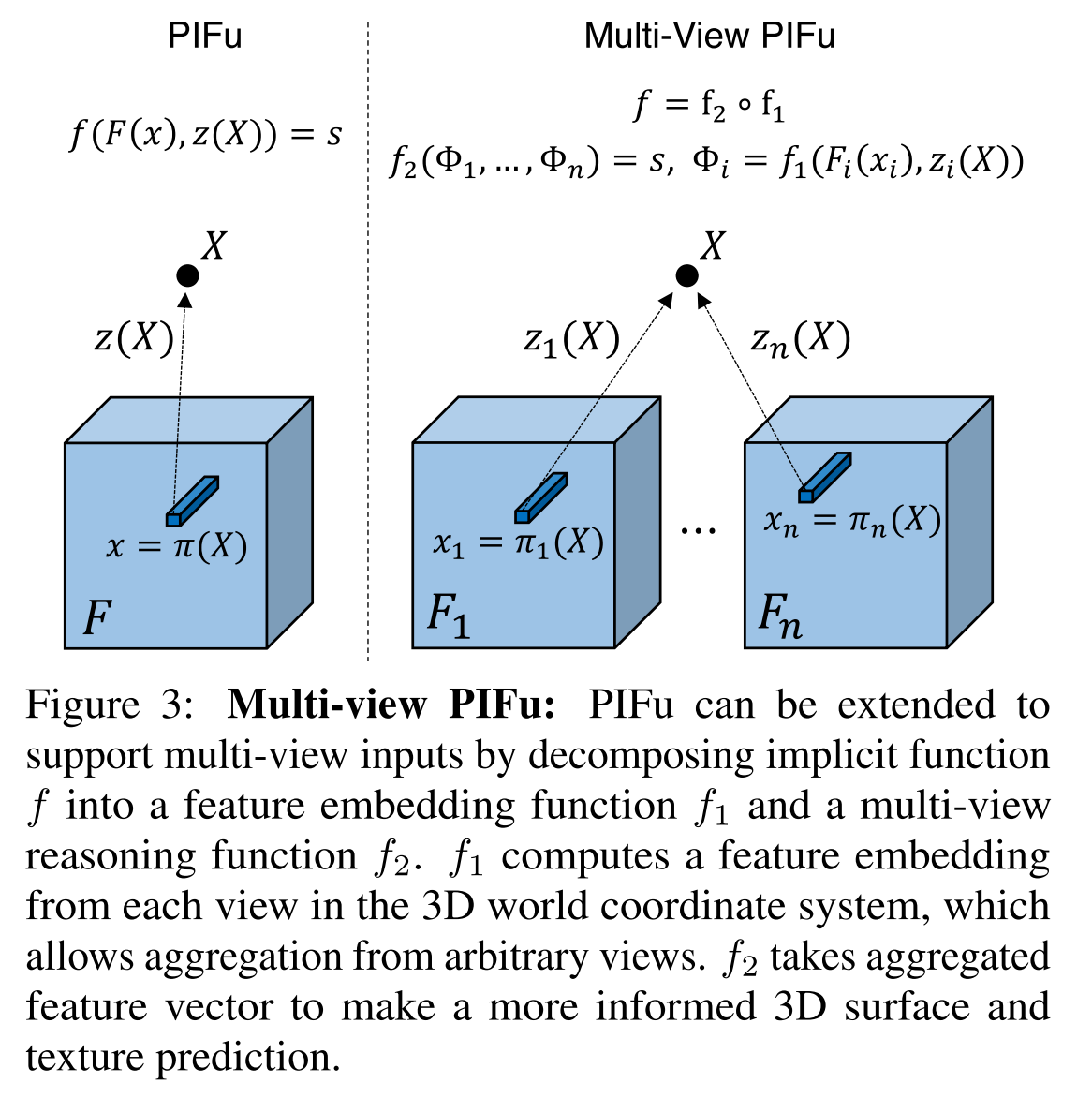
Neural Volume Rendering

Neural Volumes

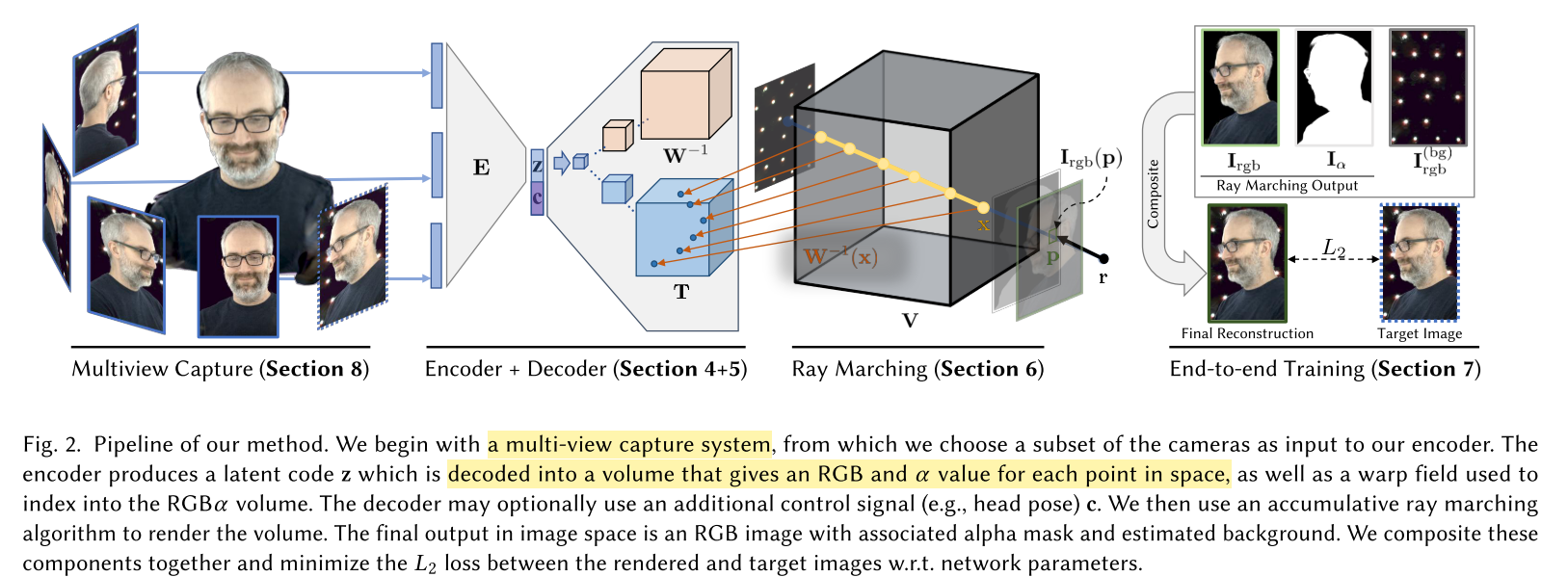
编码器(Encoder)

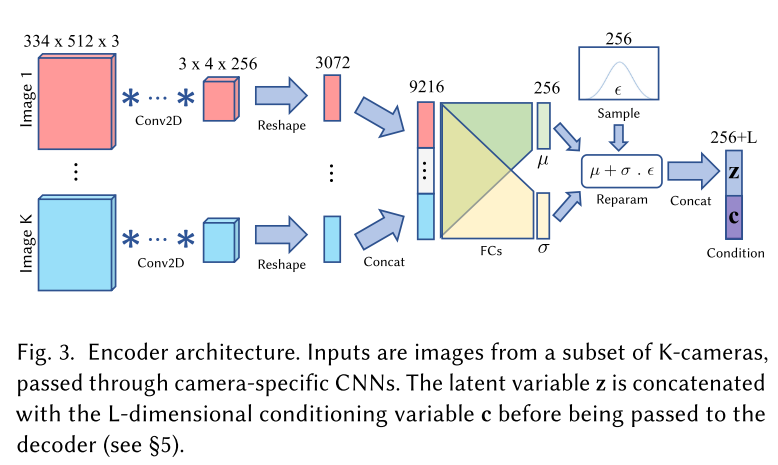
解码器(Decoder)

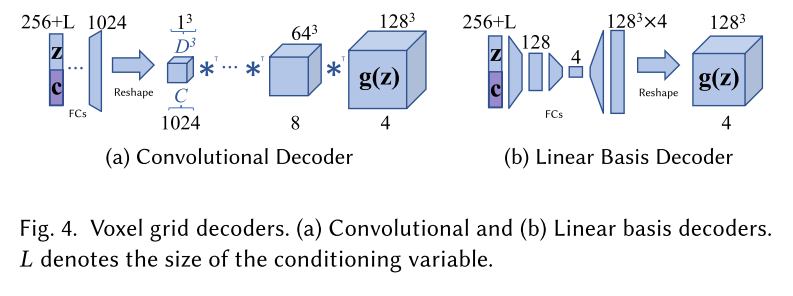
NeRF

希望通过全连接网络(多层感知机)拟合一个函数 $F_{\theta}: (\boldsymbol{x}, \boldsymbol{d}) \rightarrow (\boldsymbol{c}, \sigma)$, $(\boldsymbol{x}, \boldsymbol{d})\in R^5, (\boldsymbol{c}, \sigma)\in R^4$。 $\boldsymbol{x}\in R^3$ 表示一个三维点坐标，$\boldsymbol{d}:(\theta, \phi)$ 表示相机视角； $\boldsymbol{c}: (R, G, B)$ 表示颜色。$\sigma$ 表示不透明度。

注意：$F_\theta$ 表示的是一个静态场景。因为网络的输入只是 $(\boldsymbol{x}, \boldsymbol{d})$ 而不包含任何有关于场景的信息。因此场景信息会固化到网络的参数里面。

可以看到，这里的想法以及网络结构跟DeepSDF的非常相似，只是DeepSDF回归的是SDF值，而这里回归的是颜色和不透明度。

Volume Rendering

\[C(\mathbf{r})= \int_{t_{n}}^{t_{f}} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) d t\]

其中 $\mathbf{r}(t) = \mathbf{o} + t\mathbf{d}$ ； $T(t)=\exp \left(-\int_{t_{n}}^{t} \sigma(\mathbf{r}(s)) d s\right)$。

离散化表示为: $t_{i} \sim \mathcal{U}\left[t_{n}+\frac{i-1}{N}\left(t_{f}-t_{n}\right), t_{n}+ \frac{i}{N}\left(t_{f}-t_{n}\right)\right] \\ \hat{C}(\mathbf{r})= \sum_{i=1}^{N} T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right) \mathbf{c}_{i}, \text { where } T_{i}=\exp \left(-\sum_{j=1}^{i-1} \sigma_{j} \delta_{j}\right)$

Positional Encoding

直接的 $xyz\theta\phi$ 作为输入的话，网络无法学习到高频的信息。因此需要对位置和视角进行编码，将位置和视角映射到高位向量。 $\gamma(p)= \left(\sin \left(2^{0} \pi p\right), \cos \left(2^{0} \pi p\right), \cdots, \sin \left(2^{L-1} \pi p\right), \cos \left(2^{L-1} \pi p\right)\right)$ 这个有点类似与transformer里面的位置编码。

Hierarchical Volume sampling

不仅仅是优化一个网络，而是同事优化两个网络。一个网络是更加粗糙(coarse)的, 一个是精细(fine)的。

首先使用分层层采样采样 $N_c$ 个采样点。这 $N_c$ 个点给 coarse 的网络使用。 $\hat{C}_{c}(\mathbf{r})=\sum_{i=1}^{N_{c}} w_{i} c_{i}, \quad w_{i}=T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right)$ 然后使用逆变换采样采样 $N_f$ 个采样点。$N_c$ 和 $N_f$ 一起给 fine 的网络使用

Loss

\[\mathcal{L}=\sum_{\mathbf{r} \in \mathcal{R}} \left[\left\|\hat{C}_{c}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}+ \left\|\hat{C}_{f}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}\right]\]

NeRF++

文中分析了原来 NeRF 的潜在局限性: shape-radiance ambiguity；以及为什么原 NeRF 可以避免这个局限性得到好的结果。

提出了将背景跟前景分别使用不同的网络进行建模。

shape-radiance ambiguity

从理论上来说，从一组训练图像中优化 NeRF 中的 5D 函数可能会出现严重退化解：该函数无法在新的视角(训练集不存在的视角)下渲染得到好的图像。下图就是一个特例：

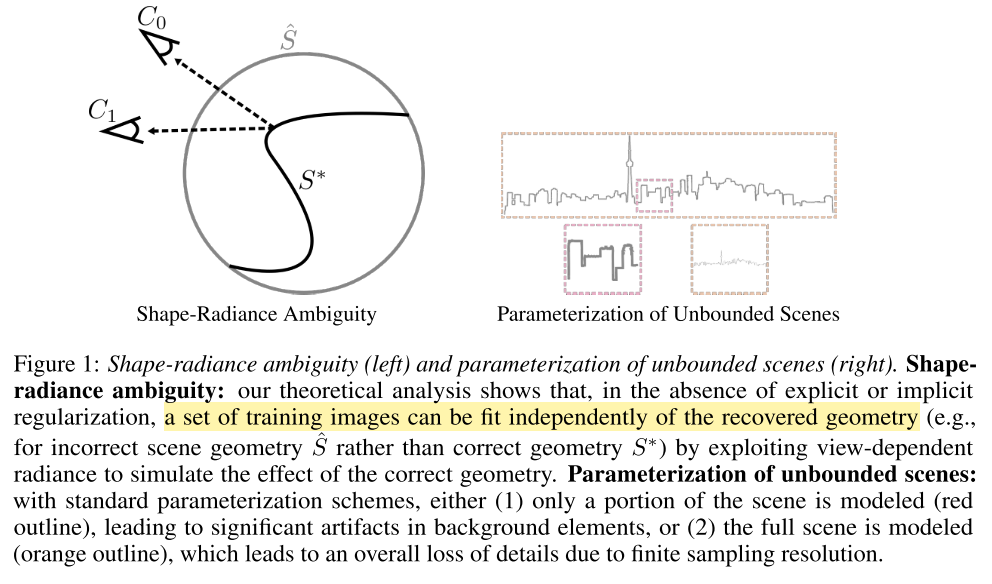
文中通过固定 NeRF 在单位球面的 $\sigma$ 为1，其他位置为零进行实验，发现在训练集中的视角可以渲染除很好的效果，但是新的视角则无法渲染得到好的效果。

为什么 NeRF 可以避免退化解

不正确的几何形状会迫使辐射场具有更高的固有复杂性(例如更高的频率)。
NeRF 的MLP 的结构隐式的蕴含着平滑的 BRDF 的先验。

对于第一点比价容易理解，当 $\sigma$ 与真实的几何结构不一致的时候，需要满足多个视角渲染约束的条件下，必然需要 $\boldsymbol{c}$ 关于视角 $\boldsymbol{d}$ 具有更高的变化频率。更高变化频率意味着需要更高的函数复杂度，而高复杂度的函数在容量有限的MLP条件下更加难以学到。

对于第二点，即 NeRF 的网络结构使得 $\boldsymbol{c}$ 关于视角 $\boldsymbol{d}$ 是一个平滑的函数。因为视角 $\boldsymbol{d}$ 是在最后一个Block才输入到网络的，那么关于视角 $\boldsymbol{d}$ 的网络容量就很小，以及视角 $\boldsymbol{d}$ 的编码也是较为低频的编码。

背景与前景分开建模

文中分析了在场景的深度范围比较小时，积分的过程可以被有限的采样点的数值过程很好的近似。但是如果是在室外场景，360°围绕一个物体的图像都可以看到周围比较远的环境，意味着场景的深度范围很大，这样就会导致无法满足 NeRF 的足够的分辨率(包括前景和背景)的要求；同时简单的采样有限的点也无法很好的近似积分过程；如果在大范围采样很多的点，时间开销是无法承受的。

文中对此提出了 inverted sphere parameterization。

具体做法是，将场景分成两个部分(Volume)：一个内单位球和一个外部反球体。

内单位球约束(建模)的是前景，外反球体约束(建模)的是环境。

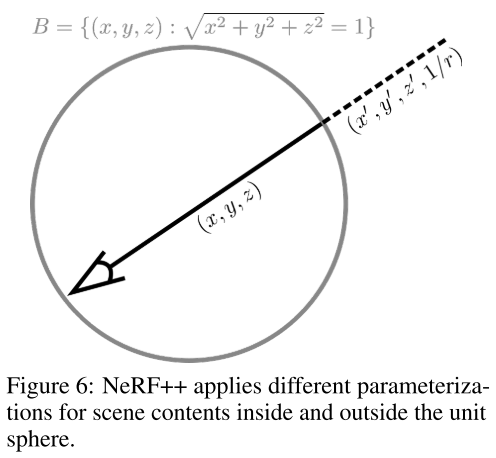
那么渲染方程变成下面式子: $\begin{aligned} \mathbf{C}(\mathbf{r})= & \underbrace{\int_{t=0}^{t^{\prime}} \sigma(\mathbf{o}+t \mathbf{d}) \cdot \mathbf{c}(\mathbf{o}+t \mathbf{d}, \mathbf{d}) \cdot e^{-\int_{s=0}^{t} \sigma(\mathbf{o}+s \mathbf{d}) d s} d t}_{(\mathrm{i})} \\ &+\underbrace{e^{-\int_{s=0}^{t^{\prime}} \sigma(\mathbf{o}+s \mathbf{d}) d s}}_{\text {(ii) }} \cdot \underbrace{\int_{t=t^{\prime}}^{\infty} \sigma(\mathbf{o}+t \mathbf{d}) \cdot \mathbf{c}(\mathbf{o}+t \mathbf{d}, \mathbf{d}) \cdot e^{-\int_{s=t^{\prime}}^{t} \sigma(\mathbf{o}+s \mathbf{d}) d s} d t}_{\text {(iii)}}. \end{aligned}$ 方程的第 $\text{i}$ 和 $\text{ii}$ 项是在欧氏空间计算的；第 $\text{iii}$ 是在反球体空间计算的，其具体计算如下：

我们首先需要计算的是 $\sigma$ 和 $\boldsymbol{c}$ 在任意的 $1/r$ 的地方。换句话来说，就是我们需要计算$1/r$ 对应的 $(x’, y’, x’)$；然后就可以将 $(x’, y’, z’, 1/r)$ 作为网络输入得到 $\sigma$ 和 $\boldsymbol{c}$ 。

对于已知的点 $\boldsymbol{p}$，其对应的 $r$ 也可以计算(即点 $\boldsymbol{p}$ 到单位球球心的距离)。那么对应的 $(x’, y’, z’)$ 可以如下图计算：

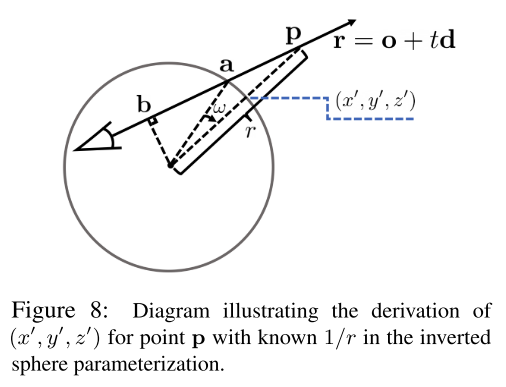
其中 $\boldsymbol{a}$ 可以用 $| \boldsymbol{o} + t_a \boldsymbol{d}| = 1$ 计算出来， $\boldsymbol{b}$ 可以用 $\boldsymbol{d}^T(\boldsymbol{o}+t_b\boldsymbol{d})=0$ 计算出来。然后我们可以将向量 $\boldsymbol{a}$ 绕着轴 $\boldsymbol{b}\times\boldsymbol{d}$ 旋转 $w = arcsin|\boldsymbol{b}| - arcsin(|\boldsymbol{b}|\cdot \frac{1}{r})$ 得到 $(x’, y’, z’)$ 。

仔细思考这个过程，可以感觉到这跟图形学里面对于环境光照的球面映射有点相似：即都是将环境映射到一个球体上面。

NeRF 后相关研究

Faster Inference

NSVF: Neural Sparse Voxel Fields

将场景(scene)组织成稀疏体素八叉树来加速场景的渲染。

采用渲染领域的光线求交的包围盒技术：BVH和SVO加速结构，以及AABB测试法。

具体做法

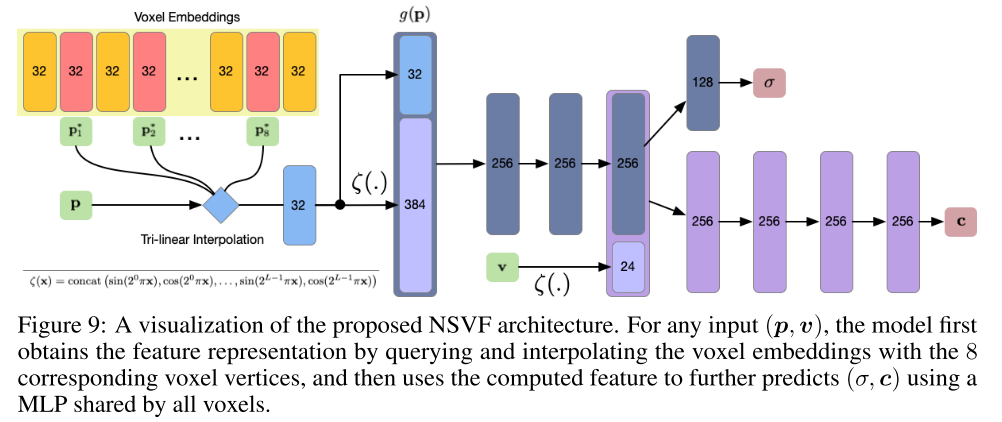
文中假设场景的非空部分可以由一组稀疏的(有界)体素表示: $\mathcal{V} = \left\{V_{1} \cdots V_{K}\right\}$。并且将场景对应建模为一系列隐函数: $F_{\theta}(\boldsymbol{p}, \boldsymbol{v})=F_{\theta}^{i}\left(\boldsymbol{g}_{i}(\boldsymbol{p}), \boldsymbol{v}\right)$ if $\boldsymbol{p} \in V_{i}$. 每一个 $F_\theta^i$ 由一个多层感知机来表示。

\[F_{\theta}^{i}:\left(\boldsymbol{g}_{i}(\boldsymbol{p}), \boldsymbol{v}\right) \rightarrow(\boldsymbol{c}, \sigma), \forall \boldsymbol{p} \in V_{i}\]

这里 $\boldsymbol{c}$ 和 $\sigma$ 是点 $\boldsymbol{p}$ 在方向 $\boldsymbol{v}$ 颜色和不透明度。 $g_i(\boldsymbol{p})$ 是点 $\boldsymbol{p}$ 的一个表示:

\[g_{i}(\boldsymbol{p})= \zeta\left(\chi\left(\widetilde{g_{i}}\left(\boldsymbol{p}_{1}^{*}\right), \ldots, \widetilde{g}_{i}\left(\boldsymbol{p}_{8}^{*}\right)\right)\right)\]

这里 $\boldsymbol{p}_{1}^{*}, \ldots, \boldsymbol{p}_{8}^{*} \in \mathbb{R}^{3}$ 是 $V_i$ 的 8个顶点。 $\widetilde{g}_{i}\left(\boldsymbol{p}_{1}^{*}\right), \ldots, \widetilde{g}_{i}\left(\boldsymbol{p}_{8}^{*}\right) \in \mathbb{R}^{d}$ 是对应的特征向量。$\chi(\cdot)$ 是三线性插值。 $\zeta(\cdot)$ 是一个后处理，在文中就是positional encoding。

与直接使用3D的坐标作为 $F_\theta^i$ 不同，这里使用的是特征向量 $g_{i}(\boldsymbol{p})$ 作为输入；而 $g_{i}(\boldsymbol{p})$ 是由八个定点的特征向量插值得到的。

Volume Rendering

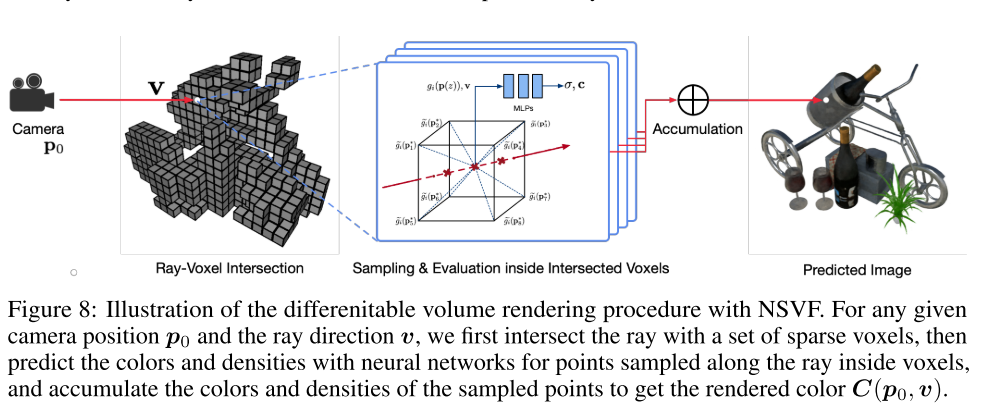
光线与体素求交：在八叉树上面运用 Axis Aligned Bounding Box intersection test (AABB 测试)。得到与对应光线相交的体素

Ray Marching inside Voxels: 只在与光线相交的区域进行采样

然后利用公式：

\[\boldsymbol{C}\left(\boldsymbol{p}_{0}, \boldsymbol{v}\right) \approx \sum_{i=1}^{N}\left(\prod_{j=1}^{i-1} \alpha\left(z_{j}, \Delta_{j}\right)\right) \cdot\left(1-\alpha\left(z_{i}, \Delta_{i}\right)\right) \cdot \boldsymbol{c}\left(\boldsymbol{p}\left(z_{i}\right), \boldsymbol{v}\right) + A(\boldsymbol{p}_0, \boldsymbol{v})\cdot \boldsymbol{c}_{bg}\]

进行像素颜色计算。 $A(\boldsymbol{p}0, \boldsymbol{v}) \cdot \boldsymbol{c}{bg}$ 是背景项，它主要目的是处理射线与所有非空体素都不相交的情况, $A\left(\boldsymbol{p}{0}, \boldsymbol{v}\right)=\prod{i=1}^{N} \alpha\left(z_{i}, \Delta_{i}\right)$, $\boldsymbol{c}_{bg}$ 是可学习的背景颜色。而 $\boldsymbol{c}$ 和 $\sigma$ 的计算通过前面的介绍方式计算，其计算图示如下：

学习过程

损失函数为：

\[\mathcal{L}= \sum_{\left(\boldsymbol{p}_{0}, \boldsymbol{v}\right) \in R} \left\|\boldsymbol{C}\left(\boldsymbol{p}_{0}, \boldsymbol{v}\right)- \boldsymbol{C}^{*}\left(\boldsymbol{p}_{0}, \boldsymbol{v}\right)\right\|_{2}^{2}+ \lambda \cdot \Omega\left(A\left(\boldsymbol{p}_{0}, \boldsymbol{v}\right)\right)\]

$\boldsymbol{C}^*$ 是 ground-truth. $\Omega(\cdot)$ 是一个 $\beta$ 分布正则化。

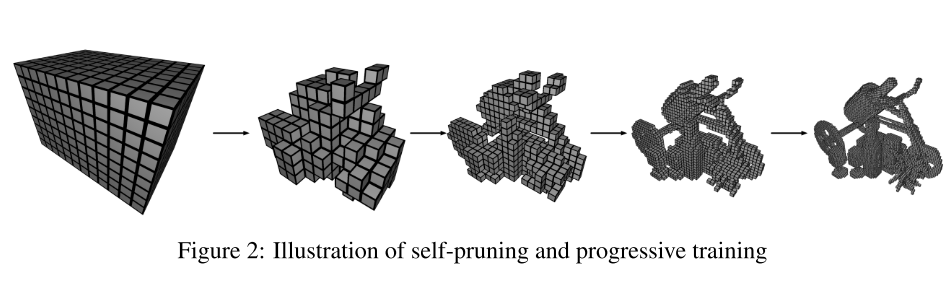
体素初始化：

初始体素大小设置为 $l \approx \sqrt[3]{V / 1000}$ 。具体可以看到上图图的最左边的一图。

自修剪：

现有的基于体积的神经渲染工作表明，在训练后在粗水平上提取场景几何是可行的。基于这一观察，文中提出了一种基于粗糙几何信息的训练过程中有效去除非必要体素的策略：自修剪；该策略可以使用模型对密度的预测来进一步描述。也就是说，我们确定要修剪的体素如下：

\[V_{i}\text { is pruned if }\min_{j=1 \ldots G} \exp \left(-\sigma\left(g_{i}\left(\boldsymbol{p}_{j}\right)\right)\right)>\gamma, \boldsymbol{p}_{j} \in V_{i}, V_{i} \in \mathcal{V}\]

这里的 $\{\boldsymbol{p}_j\}_j^G$ 是 G 个在体素 $V_i$ 均匀采样的点。文中 $G=16^3$。 $\sigma\left(g_{i}\left(\boldsymbol{p}_{j}\right)\right)$ 是网络预测的不透明度。 $\gamma$ 是一个阈值，文中取 0.5。

AutoInt

直接学的是积分的网络，从而在体素渲染的时候可以省略蒙特卡洛积分的过程；在测试阶段速度得到很大的提升。

Pipeline

具体做法就是，先构建一个全连接网络(MLP) $\Phi_\theta(\mathbf{x})$，这个网络是代表的是积分的结果；然后对这个网络利用 chain-rule 对输入 $\mathbf{x}$ 求导，构建一个梯度网络 $\Psi_\theta(\mathbf{x})$ 。需要注意的是，这里是 $\Phi_\theta(\mathbf{x})$ 对 $\mathbf{x}$ 求导，因此梯度网络 $\Psi_\theta(\mathbf{x})$ 的参数 $\theta$ 和网络 $\Phi_\theta(\mathbf{x})$ 的参数是一样的。数学方程如下：

\[\begin{array}{rcl} \Phi_{\theta}(\mathbf{x}) &= & \int \frac{\partial \Phi_{\theta}}{\partial x_{i}}(\mathbf{x}) \mathrm{d} x_{i}= \int \Psi_{\theta}^{i}(\mathbf{x}) \mathrm{d} x_{i} \\ \Psi_{\theta}^{i}&= &\partial \Phi_{\theta} / \partial x_{i} \end{array}\]

其对应的计算图如下：

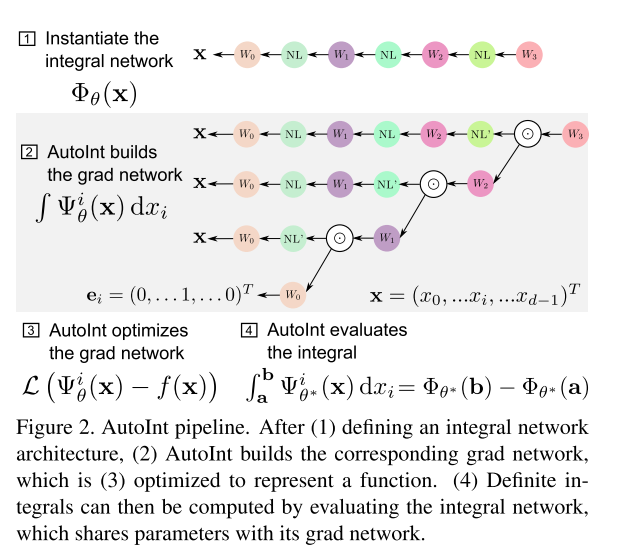
NL 为非线性激活函数。

训练方式

训练过程使用的是蒙特卡洛积分，对梯度网络进行积分，得到积分后的结果进行监督，这点其实跟原来的 NeRF 是十分相似的：这里的梯度网络 $\Psi_\theta$ 就是 NeRF 的 $F_\theta$ ，只是两者的网络结构不同而已。

\[\theta^{*}=\arg \min _{\theta} \sum_{i<D} \left\|\left(\frac{1}{T} \sum_{t_{j}<T} \Psi_{\theta}^{t}\left(\rho_{i}, \alpha_{i}, t_{j}\right)\right)- s\left(\rho_{i}, \alpha_{i}\right)\right\|_{2}^{2}\]

训练好了梯度网络之后，可以把它的参数应用到积分网络 $\Phi_\theta$ 上。测试时就可以用下式进行：

\[s(\rho, \alpha)=\Phi_{\theta^{*}}\left(\rho, \alpha, t_{f}\right)- \Phi_{\theta^{*}}\left(\rho, \alpha, t_{n}\right)\]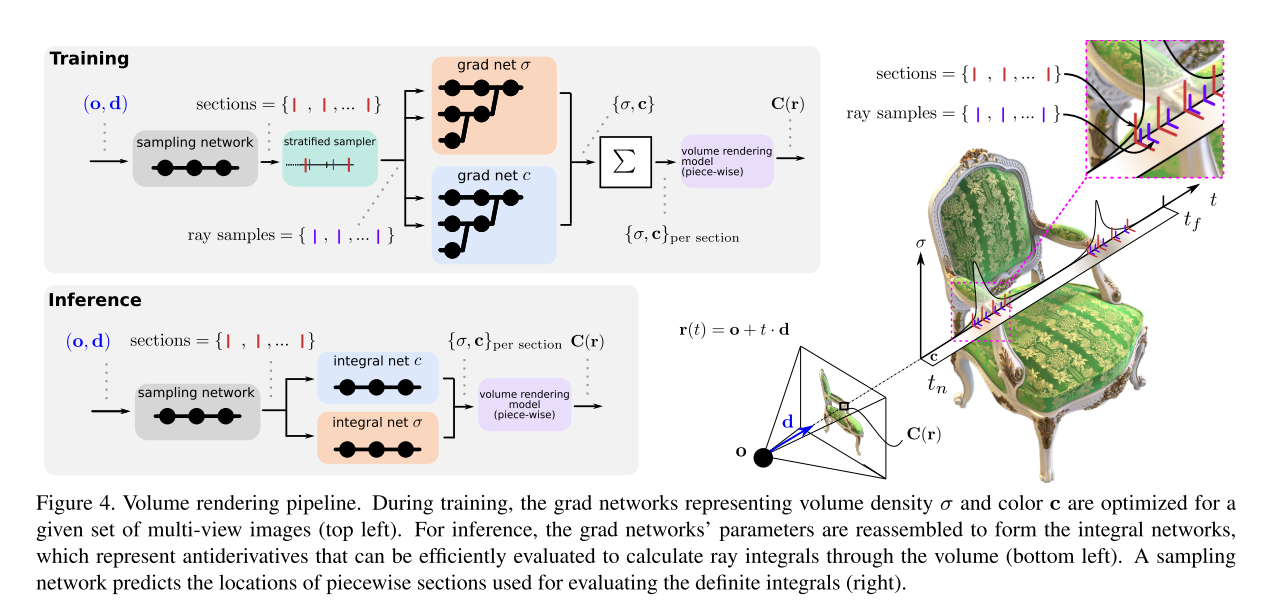

DeRF

通过将场景划分为多个区域，每个区域用更小的网络来拟合，从而利用上显卡(显存)的特性进行加速；最后通过画家算法将每个区域合并起来得到完整的场景渲染。

NeRF 的渲染

\[C(\mathbf{r})=\int_{t_{n}}^{t_{f}} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) d t\]

其中 $\mathbf{r}(t) = \mathbf{o} + t\mathbf{d}$ ； $T(t)=\exp \left(-\int_{t_{n}}^{t} \sigma(\mathbf{r}(s)) d s\right)$。

离散化表示为:

\[t_{i} \sim \mathcal{U}\left[t_{n}+\frac{i-1}{N}\left(t_{f}-t_{n}\right), t_{n}+ \frac{i}{N}\left(t_{f}-t_{n}\right)\right] \\ \hat{C}(\mathbf{r})= \sum_{i=1}^{N} T_{i}\left(1-\exp \left(-\sigma_{i} \delta_{i}\right)\right) \mathbf{c}_{i}, \text { where } T_{i}= \exp \left(-\sum_{j=1}^{i-1} \sigma_{j} \delta_{j}\right) \\ \mathcal{L}_{radiance}= \sum_{\mathbf{r} \in \mathcal{R}} \left[\left\|\hat{C}_{c}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}+ \left\|\hat{C}_{f}(\mathbf{r})-C(\mathbf{r})\right\|_{2}^{2}\right]\]

DeRFs

将辐射场 (radiance fied)函数 $\sigma(\mathbf{x})$ 和 $\mathbf{c}(\mathbf{x})$ 建模成很多个独立的函数的加权和。如图所示：

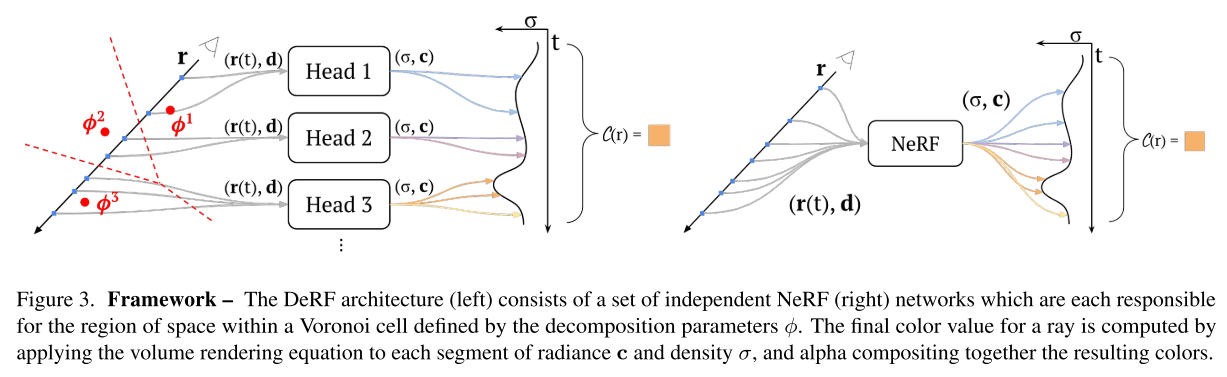
其对应的数学表达式为：

\[\begin{aligned} \sigma(\mathbf{x}) &= \sum_{n=1}^{N} w_{\phi}^{n}(\mathbf{x}) \sigma_{\theta_{n}}(\mathbf{x}) \\ \mathbf{c}(\mathbf{x}, \mathbf{d}) &= \sum_{n=1}^{N} w_{\phi}^{n}(\mathbf{x}) \mathbf{c}_{\theta_{n}}(\mathbf{x}, \mathbf{d}) \end{aligned}\]

$n$ 表示head 的index，$w_{\phi}(\mathbf{x}): \mathbb{R}^{3} \mapsto \mathbb{R}^{N}$ 表示权重函数， $\phi$ 是可学习参数，$w_{\phi}(\mathbf{x})$ 是正定的并且满足 $\left| w_{\phi}(\mathbf{x}) \right|_1 = 1$ 。

Efficient scene decomposition

将 $w_{\phi}(\mathbf{x})$ 约束成对于每个 $\mathbf{x}$，${w^n_{\phi}(\mathbf{x})}_1^N$ 里面只有一个不为0，其他的均为零。这样对于每个 $\mathbf{x}$ ，只有一个 head 需要被执行。

Balanced scene decomposition

因为所有的head具有相似的表达能力，因此对于渲染质量来说，更好的划分方式是将场景的信息较为均匀的进行划分。

引入 $\mathcal{W}_{\phi}(\mathbf{r}) \in \mathbb{R}^{N}$ 表示对于特定的一条光线，N 个head的总贡献。

\[\mathcal{W}_{\phi}(\mathbf{r})=\int_{t_{n}}^{t_{f}} \mathcal{T}(t) \sigma(\mathbf{r}(t)) w_{\phi}(\mathbf{r}(t)) d t\]

然后通过最小化以下约束来使得N个head对于场景的信息贡献更加平均：

\[\mathcal{L}_{\text {uniform }}= \left\|\mathbb{E}_{\mathbf{r} \sim R}\left[\mathcal{W}_{\phi}(\mathbf{r})\right]\right\|_{2}^{2}\]

这里N个head对于场景的信息贡献更加平均，并不是说 N 个 head 在场景的空间上的权重均匀；而恰恰相反，N 个 head 在空间划分上的权重应该是每个 head 集中到某个特定的区域，而其他区域权重趋于0。

这里有点难以理解。 $\mathcal{L}_{uniform}$ 是均值向量的二范数，而因为 $\left\| w_{\phi}(\mathbf{x}) \right\|_1 = 1$，所以 $\|\mathcal{W}_{\phi}(\mathbf{r})\|_1$ 是与参数 $\phi$ 无关的，只与 $\sigma$ 有关。对于一个特定场景, $\sigma$ 的关于位置分布是确定的，那么想要 $\mathcal{L}_{\text {uniform }}=\left\|\mathbb{E}_{\mathbf{r} \sim R} \left[\mathcal{W}_{\phi}(\mathbf{r})\right]\right\|_{2}^{2}$ 最小，则应该使得每个head(即 $\mathcal{W}_\phi(\mathbf{r})$ 的一个维度) 只对特定一个区域位置有集中的权重响应，其他区域权重趋于零。

Voronoi learnable decompositions

上面说到的是将 radiance field 函数划分为N个小的函数(heads)，以及怎么使得N个小的函数(heads)在信息表示上具有想要的特点(测试时更加高效的或者信息表达更加均匀分配的)。

而上面的这些并没有对于在空间上的划分的任何约束或者或规则。这部分就是说如何约束 N 个小函数表达不同的空间划分的。

文中是将场景划分为沃罗诺伊图(Voronoi)。为了参数可学习，文中划分的是soft-Voronoi。其划分的数学表达式如下： $w_{\phi}^{n}(\mathbf{x})= \frac{e^{-\beta \| \mathbf{x}-\phi^{n} \|_{2}}} {\sum_{j=1}^{N} e^{-\beta\left\|\mathbf{x}-\phi^{j}\right\|_{2}}}$ $\beta \in \mathbb{R}^+$ 是一个超参数，它控制着 Voronoi 图划分的 softness。

Compose

因为 Voronoi 图是适用画家算法(Painter Algorithm)的，可以使用画家算法进行渲染场景的组合。

训练细节

文中作者发现，在训练 $\sigma_{\theta_n}$ 和 $\mathbf{c}_{\theta_n}$ 之前，必须先把 $w_{\phi}$ 训练好；但是如方程 $\mathcal{W}_{\phi}(\mathbf{r})=\int_{t_{n}}^{t_{f}}\mathcal{T}(t) \sigma(\mathbf{r}(t)) w_{\phi}(\mathbf{r}(t)) d t$ 所示，要训练 $w_{\phi}$ 需要知道 $\sigma$。

因此作者先训练一个粗糙的全场景的 $\sigma_{coarse}$ 和 $\mathbf{c}_{coarse}$, 然后训练 $w_\phi$ 在训练的过程中，其实这两个是交替训练的，即 $\mathcal{L}_{radiance}$ 和 $\mathcal{L}_{uniform}$ 交替优化。

优化好 $w_\phi$ 之后，训练每个 DeRFs $\sigma_{\theta_n}$ 和 $\mathbf{c}_{\theta_n}$ 时，参数 $\phi$ 是固定的。

对于参数 $\beta$ 的调节

刚开始训练的时候，$\beta$ 比价小，使得 $w^i(\mathbf{x}) \approx w^j(\mathbf{x})$ ；随着训练推进，指数级的增加 $\beta$ 直到达到设定的阈值。这个过程就是使得 Voronoi 划分 soft 到 hard。最后的 $\beta$ 的值应使得 Voronoi 划分非常接近 hard 的划分，即 $w^i(\mathbf{x}) \approx 1$ 或 $w^i(\mathbf{x}) \approx 0$，这样才能更加适用画家算法。

Unconstrained Images

NeRF in the Wild

原来 NeRF 假设(要求)场景在几何，光照是静态。这就要求场景的图片是在短时间内拍摄出来的，这样才满足静态场景的要求；如果图片拍摄的间隔时间长，那么场景中的光照和物体都可能发生了变化。这个假设/要求大大限制了 NeRF 的适用范围。

文中提出的 NeRF-W 将场景的静态部分和动态部分分开建模。建模的方式就是将可变的部分表示为一个 Embedded vector (是一个可优化变量，跟着网络一起优化)，其思想来源是 Generative Latent Optimization 这篇文章。

Background(NeRF)

\[\begin{aligned} \hat{\mathbf{C}}(\mathbf{r})&=\mathcal{R}(\mathbf{r}, \mathbf{c}, \sigma) = \sum_{k=1}^{K} T\left(t_{k}\right) \alpha\left(\sigma\left(t_{k}\right) \delta_{k}\right) \mathbf{c}\left(t_{k}\right) \\ \text{where} \, T\left(t_{k}\right) &= \exp \left(-\sum_{k^{\prime}=1}^{k-1} \sigma\left(t_{k^{\prime}}\right) \delta_{k^{\prime}}\right) \\ [\sigma(t), \mathbf{z}(t)] &= \operatorname{MLP}_{\theta_{1}} \left(\gamma_{\mathbf{x}}(\mathbf{r}(t))\right) \\ \mathbf{c}(t) &=\operatorname{MLP}_{\theta_{2}} \left(\mathbf{z}(t), \gamma_{\mathbf{d}}(\mathbf{d})\right) \end{aligned}\]

同时训练一个coarse一个fine 网络来提高采样的效率。对应的loss函数如下：

\[\mathcal{L} = \sum_{i j}\left\|\mathbf{C}\left(\mathbf{r}_{i j}\right)- \hat{\mathbf{C}}^{c}\left(\mathbf{r}_{i j}\right)\right\|_{2}^{2} \quad +\left\|\mathbf{C}\left(\mathbf{r}_{i j}\right)- \hat{\mathbf{C}}^{f}\left(\mathbf{r}_{i j}\right)\right\|_{2}^{2}\]

网络结构

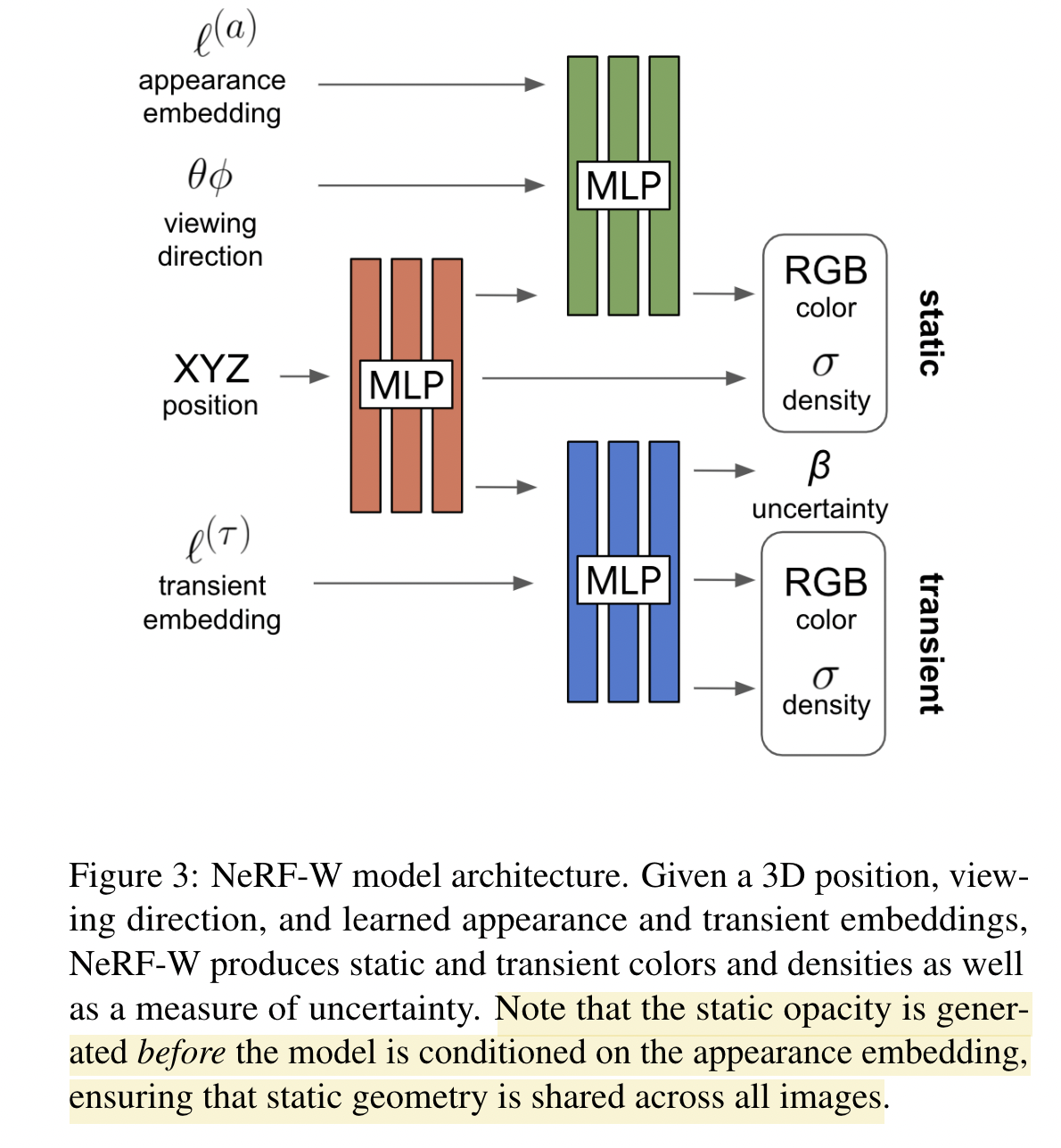
Latent Apperance Modeling

每张图片 $\mathcal{I}_i$ 都对应着一个自己的 Embedded vector $\boldsymbol{\ell}_{i}^{(a)}$，这是一个 $n^a$ 维的向量。

这样子对应的渲染公式就变成如下：

\[\begin{array}{c} \hat{\mathbf{C}}_{i}(\mathbf{r})= \mathcal{R}\left(\mathbf{r}, \mathbf{c}_{i}, \sigma\right) \\ \mathbf{c}_{i}(t)=\operatorname{MLP}_{\theta_{2}} \left(\mathbf{z}(t), \gamma_{\mathbf{d}}(\mathbf{d}), \ell_{i}^{(a)}\right) \end{array}\]

Embedded vector $\boldsymbol{\ell}_{i}^{(a)}$ 跟着网络参数 $\theta$ 一起优化。

Transient Object

对于原来的 NeRF 结构，只能建模静态物体的场景。为了可以建模场景里面的有些物体发生变化(出现或消失)的场景，我们在原来 NeRF 结构的基础上，添加一个用来建模“短暂”存在的物体的 head。同时，不再假设对于图片中的每一个像素都具有同等的可信度，而是让 Transient head 输出一个不确信度场(实际上输出的是方差)。

在文中是将每个像素的颜色建模成各向同性的正态分布，网络训练的一个就是最大化这个分布的似然函数。

对于 transient head 的东西，也是跟 NeRF 一样渲染，然后与静态的部分加起来。整个的网络渲染公式如下：

\[\begin{array}{c} \hat{\mathbf{C}}_{i}(\mathbf{r})= \sum_{k=1}^{K} T_{i}\left(t_{k}\right) \left(\alpha\left(\sigma\left(t_{k}\right) \delta_{k}\right) \mathbf{c}_{i}\left(t_{k}\right)+\alpha\left(\sigma_{i}^{(\tau)}\left(t_{k}\right) \delta_{k}\right) \mathbf{c}_{i}^{(\tau)}\left(t_{k}\right)\right) \\ \text { where } T_{i}\left(t_{k}\right)= \exp \left(-\sum_{k^{\prime}=1}^{k-1}\left(\sigma\left(t_{k^{\prime}}\right)+ \sigma_{i}^{(\tau)}\left(t_{k^{\prime}}\right)\right) \delta_{k^{\prime}}\right) \end{array}\]

对于不确定度采用的是贝叶斯学习框架来建模。假设观察到的像素强度本质上是嘈杂的，而且该噪声是与输入有关的(异方差的)。将像素的观测颜色 $\boldsymbol{C}_i(\mathbf{r})$ 建模成一个与 image 和光线都有关的各向同性正态分布，均值是网络输出 $\hat{\boldsymbol{C}}_i(\mathbf{r})$ ，方差是 $\beta_i^2(\mathbf{r})$:

$\hat{\beta}_{i}(\mathbf{r})= \mathcal{R}\left(\mathbf{r}, \beta_{i}, \sigma_{i}^{(\tau)}\right)$ $\beta_i$ 为网络 transient head 的一个输出： $\begin{array}{c} {\left[\sigma_{i}^{(\tau)}(t), \mathbf{c}_{i}^{(\tau)}(t), \tilde{\beta}_{i}(t)\right]= \operatorname{MLP}_{\theta_{3}}\left(\mathbf{z}(t), \ell_{i}^{(\tau)}\right)} \\ \beta_{i}(t)=\beta_{\min }+\log \left(1+\exp \left(\tilde{\beta}_{i}(t)\right)\right) \end{array}$

网络的 Loss 为：

\[L_{i}(\mathbf{r})= \frac{\left\|\mathbf{C}_{i}(\mathbf{r})-\hat{\mathbf{C}}_{i}(\mathbf{r})\right\|_{2}^{2}} {2 \beta_{i}(\mathbf{r})^{2}}+ \frac{\log \beta_{i}(\mathbf{r})^{2}}{2}+\frac{\lambda_{u}}{K} \sum_{k=1}^{K} \sigma_{i}^{(\tau)}\left(t_{k}\right)\]

Optimization

优化的时候，跟原来的 NeRF 一样同时寻来呢一个 coarse 和一个fine 网络。但是 coarse 网络就是跟原来 NeRF 的网络是一样的，而不是文中修改后的网络。其完整的loss 如下：

\[\sum_{i j} L_{i}\left(\mathbf{r}_{i j}\right)+ \frac{1}{2}\left\|\mathbf{C}\left(\mathbf{r}_{i j}\right)- \hat{\mathbf{C}}_{i}^{c}\left(\mathbf{r}_{i j}\right)\right\|_{2}^{2}\]