准确率
$Acc = \frac{n_{correct}}{n_{total}}$
当类别样本极其不均衡时,占比大的类别成为影响准确率的主要因素,占比小的类别的作用几乎完全被忽略。
精确率和召回率
$Precision = \frac{TP}{TP+FP}, \,\,\, Recall = \frac{TP}{TP+FN}$
P-R 曲线
以召回率(R)为横坐标,精确率(P)为纵坐标.
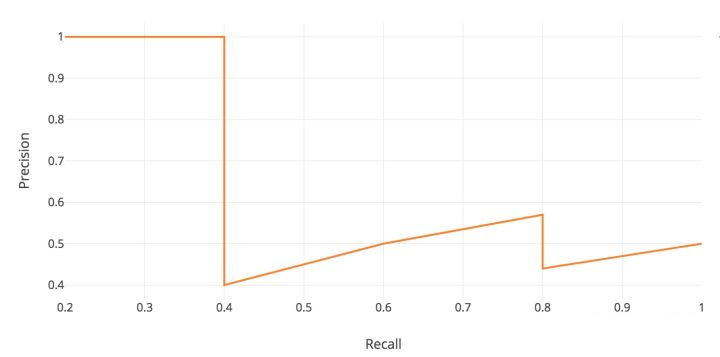
AP(average precision)
顾名思义 AP 就是平均精准度,简单来说就是对 PR 曲线上的 Precision 值求均值。 对于 pr 曲线来说,我们使用积分来进行计算: $AP = \int_0^1 p(r)dr$。
在实际应用中,我们并不直接对该 PR 曲线进行计算,而是对 PR 曲线进行平滑处理。 即对 PR 曲线上的每个点,Precision 的值取该点右侧最大的 Precision 的值。
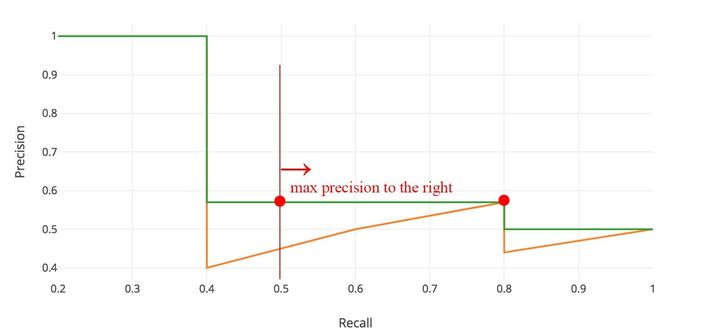
用公式来描述就是$P_{smooth}(r) = max_{r’>=r} P(r’)$。用该公式进行平滑后再用上述公式计算 AP 的值。
Interpolated AP (Pascal Voc 2008)
Pascal VOC 2008 中设置 IoU 的阈值为 0.5,如果一个目标被重复检测,则置信度最高的为正样本, 另一个为负样本。在平滑处理的 PR 曲线上,取横轴 0-1 的 10 等分点(包括断点共 11 个点)的 Precision 的值, 计算其平均值为最终 AP 的值:
\[AP = \frac{1}{11}\sum_{0,0.1,\cdots,1.0} P_{smooth}(i)\]Area under curve
上述方法有两个缺陷,第一个是使用 11 个采样点在精度方面会有损失。第二个是,在比较两个 AP 值较小的模型时, 很难体现出两者的差别。所以这种方法在 2009 年的 Pascalvoc 之后便不再采用了。 在 Pascal voc 2010 之后,便开始采用这种精度更高的方式。绘制出平滑后的 PR 曲线后, 用积分的方式计算平滑曲线下方的面积作为最终的 AP 值。
\[AP = \int_0^1 P_{smooth}(r) dr\]COCO mAP
最新的目标检测相关论文都使用 coco 数据集来展示自己模型的效果。对于 coco 数据集来说, 使用的也是 Interplolated AP 的计算方式。与 Voc 2008 不同的是, 为了提高精度,在 PR 曲线上采样了 100 个点进行计算。 而且 Iou 的阈值从固定的 0.5 调整为在 0.5 - 0.95 的区间上每隔 0.5 计算一次 AP 的值, 取所有结果的平均值作为最终的结果。
ROC 曲线
横坐标为假阳性率: $FPR = \frac{FP}{N}$,
纵坐标为真阳性率: $TPR = \frac{TP}{P}$ ,(召回率)
绘制 ROC 曲线
从大到小移动分类器阈值,得到每个阈值对应的 FPR 和 TPR。在 ROC 图上绘制出每个阈值点的位置,再连起来就得到了 ROC 曲线。
AUC
AUC 指 ROC 曲线下方的面积,该值能够量化的反映基于 ROC 曲线衡量的模型性能。
由于 ROC 曲线一般位于 y=x 的上方(如果不是的话,将分类器的概率取反 1-p),因此 AUC 在[0.5, 1]之间。
ROC 曲线与 P-R 曲线的特点
相比于 P-R 曲线,ROC 曲线在正负样本的分布发生变化时,ROC 曲线的形状能够基本不改变;而 P-R 曲线的形状往往发生剧烈变化。
余弦距离
余弦相似度:
\[cos(A, B) = \frac{A\cdot B}{\left|A\right|_2 \left| B \right|_2}\]相对于欧氏距离,余弦相似度不受维度的影响。
余弦距离:
\[dist(A, B) = 1 - cos(A, B) = 1 - \frac{A\cdot B}{\left| A \right|_2 \left| B \right|_2}\]如果向量模长经过归一化,欧氏距离与余弦距离具有单调关系: $|A-B| = \sqrt{2(1-cos(A, B))}$.
余弦距离不是一个严格定义的距离,满足 1. 正定性, 2. 对称性, 不满足 3. 三角不等式。
A/B 测试
A/B 测试的必要性
- 离线评估无法完全消除模型过拟合的影响,因此得出的离线评估结果无法完全替代线上评估的结果。
- 离线评估无法完全还原线上的工程环境。一般来讲,离线评估往往不会考虑线上环境的延迟、数据丢失、标签数据缺失等情况。因此离线评估的结果是理想工程环境下的结果。
- 线上系统的某些商业指标在离线评估中无法计算。
A/B 测试方法
进行 A/B 测试的主要手段是进行用户分桶,即将用户分为实验组和对照组。对实验组的用户使用新模型,对照组用户使用旧模型。分桶过程需要注意:
- 样本的独立性 (一个用户仅在一个桶)
- 采样方式的无偏性
- 仅针对满足特定条件的用户分桶(否则结果可能会被稀释)
模型评估方法
holdout 检验
holdout 检验即留出检验,是最简单最直接的检验方法。
将原始数据集随机分成训练集和验证集两部分。一般划分比例为 7:3。
交叉验证
k-fold 交叉验证: 首先将数据集划分成 k 个大小相等的数据子集; 依次遍历这 k 个子集,每次把当前子集当做验证集,其余所有当做训练集进行模型训练和评估。 最后把 k 次评估指标的平均值作为最终的评估指标。k 经常取 10.
留一验证:每次留下 1 个样本作为验证集,其余数据全部作为训练集。 样本总数为 n,依次对 n 个样本遍历,进行 n 次模型训练和验证,将 n 次评估指标求平均得到最终指标。时间复杂度为 O(n)。
自助法
对于数据集较小的情况下,Holdout 和交叉验证的数据划分会使得训练数据更加少。 自助法基于自助采样,对于总数为 n 的样本集合,进行 n 次又放回抽样,得到大小为 n 的训练集。 n 次采样中,有的样本重复采样,有的没有被采样到;没有被采样到的样本作为验证集。 n 趋于无穷大时,大约有 36.8%的数据没有被采样到。
超参数调优
网格搜索
最简单直接的方法:通过查找搜索范围内所有的点来确定最优值。
如果采用较大搜索范围和较小步长,很有可能搜索到全局最优。但是十分消耗计算资源和时间。
一般是:先较大搜索范围和较大步长,搜索全局最有最可能的位置;再逐步缩小搜索范围和步长, 寻找更精确的最优值。可以缩短搜索时间,但是由于目标函数一般是非凸的,可能会错过全局最优解。
随机搜索
思想与网格搜索类似,只是不是测试范围内所有的点,而是在搜索范围内随机采样搜索点。
理论依据是如果采样点数足够,那么随机采样大概率地找到全局最有值。
贝叶斯优化算法
与网格搜索和随机搜索不同完全不同。 网格搜索和随机搜索在测试一个新点时,会忽略前一个点的信息;而贝叶斯优化算法则充分利用了之前搜索点的信息。
贝叶斯优化算法通过对目标函数形状进行学习,找到使目标函数全局最优值提升的参数。
具体是,首先根据先验分布,假设一个搜集函数;然后每一次使用新的采样点来测试目标函数时, 利用这个信息来更新目标函数的先验分布;最后,算法测试由后验分布给出全局最值最可能出现的位置的点。
需要注意的是,贝叶斯优化算法一旦找到一个局部最优值,它会不断在该区域进行采样, 所以很容易陷入局部最优。因此需要加上“探索”(在未取样的区域采样)的因素。






