-
Sigmoid
Sigmoid激活函数也叫做Logistic函数,因为它是线性回归转换为Logistic(逻辑回归)的核心函数, 这也是Sigmoid函数优良的特性能够把X ∈ R的输出压缩到X ∈ (0, 1)区间。
Sigmoid激活函数在其大部分定义域内都会趋于一个饱和的定值。 当x取绝对值很大的正值的时候,Sigmoid激活函数会饱和到一个高值(1); 当x取绝对值很大的负值的时候,Sigmoid激活函数会饱和到一个低值(0)。 Sigmoid函数是连续可导函数,在零点时候导数最大,并在向两边逐渐降低, 可以简单理解成输入非常大或者非常小的时候,梯度为0没有梯度,如果使用梯度下降法,参数得不到更新优化。
\[f(z) = \frac{1}{1+e^{-z}} \\ f'(z) = f(z)(1-f(z)) = \frac{e^{-z}}{(1+e^{-z})^2}\]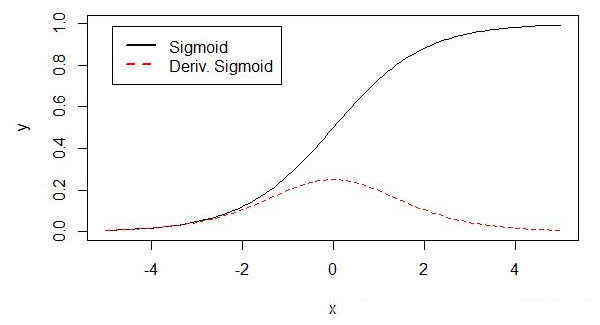
Sigmoid函数最大的特点就是将数值压缩到(0, 1)区间,在机器学习中常利用(0, 1)区间的数值来表示以下意义:
-
概率分布:根据概率公理化定义知道,概率的取值范围在[0, 1]之间, Sigmoid函数的(0, 1)区间的输出和概率分布的取值范围[0, 1]契合。 因此可以利用Sigmoid函数将输出转译为概率值的输出。这也是Logistic(逻辑回归)使用Sigmoid函数的原因之一;
-
信号强度:一般可以将0~1理解成某种信号的强度。 由于RNN循环神经网络只能够解决短期依赖的问题,不能够解决长期依赖的问题, 因此提出了LSTM、GRU,这些网络相比于RNN最大的特点就是加入了门控制, 通过门来控制是否允许记忆通过,而Sigmoid函数还能够代表门控值(Gate)的强度, 当Sigmoid输出1的时候代表当前门控全部开放(允许全部记忆通过), 当Sigmoid输出0的时候代表门控关闭(不允许任何记忆通过)。
上面介绍了Sigmoid激活函数将输出映射到(0, 1)区间在机器学习中的两个意义, 这也是Sigmoid激活函数的优点。接下来介绍一下Sigmoid激活函数的缺点:
-
经过Sigmoid激活函数输出的均值为0.5,即输出为非0均值;
反向传播时候更新方向要不往正向更新,要不往负向更新,会导致捆绑效果, 使得收敛速度减慢。当然,如果使用小批量梯度下降法,由于每个小batch可能会得到不同的信号, 所以这个问题还是有可能缓解的。2015年loffe提出的批标准化(Batch Normalization) 就是为了适应性的将每层输出分布都进行统一,以便网络学习更加稳定、更快的传播。
-
-
Tanh
\[f(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}} \\ f'(z) = 1 - (f(z))^2 = \frac{4}{(e^z + e^{-z})^2}\]Tanh激活函数(hyperbolic tangent, 双曲正切),通过函数表达式可以看出,tanh可由sigmoid激活函数平移缩放得到。
\[tanh(x) = 2 sigmoid(2x) - 1\]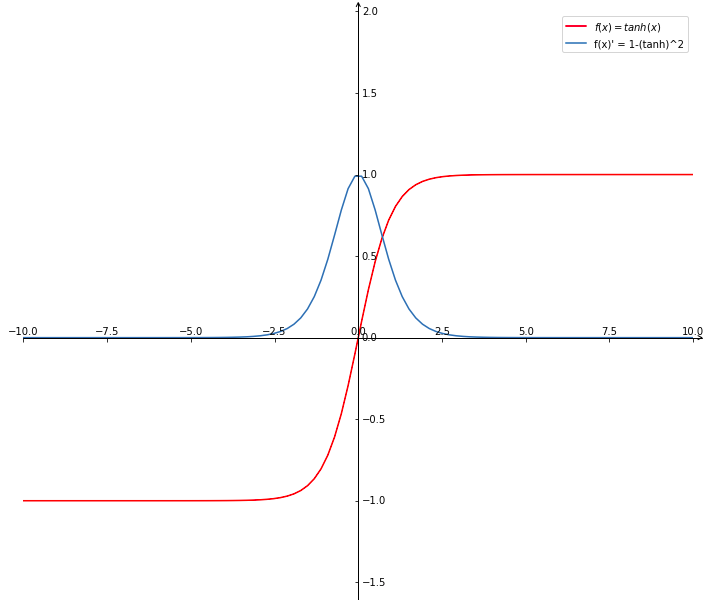
tanh函数将输出值映射到(-1, 1)区间,有点类似于幅度增大的sigmoid激活函数。
优点:
- 输出均值为0。这是tanh非常重要的一个优点;
- tanh在原点附近与y = x函数形式相近,当激活值比较低的时候,训练相对比容易;
- tanh的变化敏感区间较宽,缓解梯度弥散的现象。tanh导数取值范围在0到1之间,要优于sigmoid激活函数的0到0.25, 相比于Sigmoid激活函数能够缓解梯度弥散的现象;
- tanh的输出和输入能够保持非线性单调上升和下降的关系,符合反向传网络梯度的求解,容错性好,有界;
缺点:
- 计算量比较大;
-
ReLU
\[f(z) = \max(0, z) \\ f'(z) = \left\{\begin{matrix} 1, \quad z>0\\ 0, \quad z \leq 0 \end{matrix}\right.\]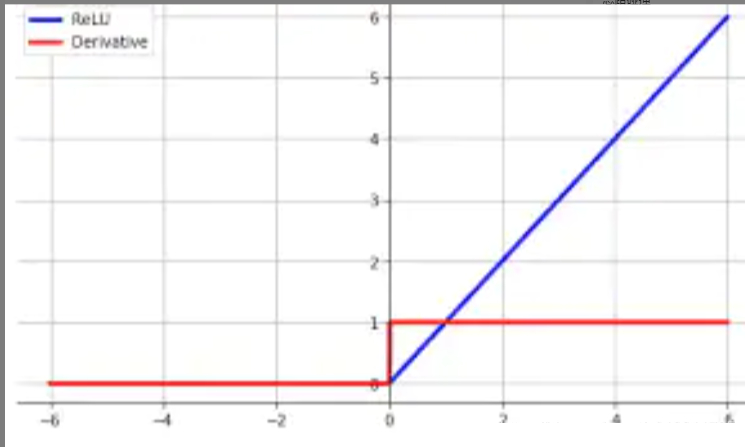
优点:
- 从计算角度,Sigmoid 和 Tanh 均需要计算指数,计算复杂度高,而 ReLU 只需要进行阈值判断即可。
- ReLU 的非饱和性可以有效解决梯度消失问题,提供相对宽的激活边界。
- ReLU 的单侧抑制能力提供了网络的稀疏表达能力。
缺点:
- 训练过程中会导致神经元死亡。 这是由于函数 $f(z) = \max(0, z)$ 在 z 为负时,梯度为 0。 在实际训练中,如果学习率设置过大,会导致一定比例神经元不可逆死亡,进而参数梯度无法更新,整个训练过程失败。
-
Leaky ReLU
为了解决上述 ReLU 的问题,设计了 Leaky ReLU:
\[f(z) = \left\{\begin{matrix} z, \quad z>0 \\ az, \quad a\leq 0 \end{matrix}\right.\]$a$ 是一个很小的正数(常数)。这样即实现了单侧抑制,有保留了部分负梯度信息。使得神经元死亡问题得到改善。
-
Parametric ReLU (PReLU)
将 Leaky ReLU 的参数$a$ 作为一个可学习的参数,在网络训练中一起参与优化。
-
Random ReLU (RReLU)
在训练过程中,Leaky ReLU 的斜率参数 $a$ 作为一个满足某种分布的随机采样;测试再固定下来。
-
Swish
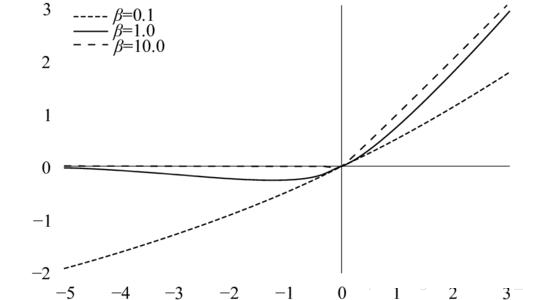
Swish是谷歌在17年提出的一个激活函数,形式非常简单,几乎就是Sigmoid和ReLU的拼凑, 具备无上界有下界、平滑、非单调的特性,性能在总体上优于ReLU。
\[f(z) = z\cdot sigmoid(\beta z)\]$\beta$ 是一个超参数。其不同取值对应图像如下:
-
Mish
与Swish类似,Mish 则是ReLU 与 Tanh 结合在一起的产物。
\[f(z) = z \cdot tanh(ln(1+e^z))\]Mish 没有超参数,其图像如下:
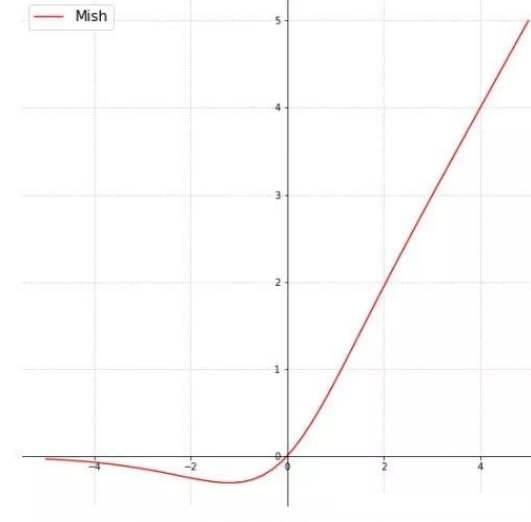
可以看到与 Swish 在 $\beta = 1$ 时是函数的图像趋势是比较相似的。






