153. Find Minimum in Rotated Sorted Array

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

Find the minimum element.

You may assume no duplicate exists in the array.

Example 1:

Input: [3,4,5,1,2] 
Output: 1

Example 2:

Input: [4,5,6,7,0,1,2]
Output: 0

解题思路：

这题如果按照$O(n)$的复杂度做的话，是十分简单的。只要遍历一次数组就可以了。 但是我们可以找到更加优秀的算法。由于数组是”有序”的，只是经过了一个旋转。 如果我们画出数组里面的元素的图的话，大概如下：

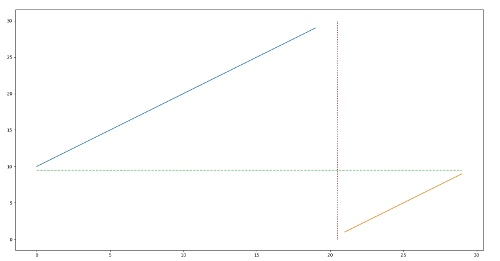
其中蓝的和橙色的线段表示数据，另外的横和竖的虚线是标线。 这就是我们拿到的数组的数据的情况。我们要找的最小的元素就是橙色线段的最左边的那个点。 很显然我们还是可以利用二分查找的。 如果 $nums[r] < nums[mid]$, 那么说明 $l, mid$位于蓝色线段上，因此 $l=mid+1$ ， 否则$ mid$ 位于橙色线段上，$r = mid$ ,(这里要注意的是r=mid，而不是r=mid-1，因为有可能会越过边界). 代码如下：

class Solution {
public:
    int findMin(vector<int>& nums) 
    {
        int l = 0;
        int r = nums.size() -1;
        if(nums[l] < nums[r])
            return nums[l];
        while(l<r)
        {
            int mid = (l+r)/2;
            if(nums[mid] > nums[r])
                l = mid + 1;
            else
                r = mid;
        }
        return nums[l];
    }
};

154. Find Minimum in Rotated Sorted Array II

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

Find the minimum element.

The array may contain duplicates.

Example 1:

Input: [1,3,5]
Output: 1

Example 2:

Input: [2,2,2,0,1]
Output: 0

Note:

• This is a follow up problem to Find Minimum in Rotated Sorted Array.
• Would allow duplicates affect the run-time complexity? How and why?

解题思路

这题是基于上一题的，但是不同的是，这里允许有重复的元素。 这个变化会带来更加麻烦的二分查找的边界处理。

class Solution {
public:
    int findMin(vector<int>& nums) 
    {
        int l = 0;
        int r = nums.size() -1;
        if(nums[l] < nums[r])
            return nums[l];
        while(l<r)
        {
            int mid = (l+r)/2;
            if(nums[mid] > nums[r])
                l = mid + 1;
            else if(nums[mid] < nums[r])
                r = mid;
            else
                r = r-1;
        }
        return nums[l];
    }
};